11
IRRATIONAL NUMBERS
The relationship of arithmetic to geometry
The square drawn on the diagonal
The invention of irrational numbers
THE JOB OF ARITHMETIC when confronted with geometry is to provide a number -- a name -- for every ratio of magnitudes. Thus, if we say that a length is 3½ meters, then the number 3½ names the ratio of
that length to 1 meter. (Lesson 7.) Some other length might be 3/8 of a meter, or 6.314 times it, and so on. The names of numbers indicate ratios to some unit.
But is there a number to indicate or name every ratio? If the square
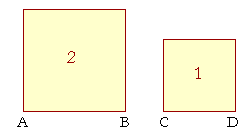on AB is to the square on CD in the ratio 2 : 1, then AB, CD themselves are incommensurable; 2 and 1 are not both square numbers; and no rational number can indicate the ratio of those sides. For, any two rational numbers always have a common measure. Incommensurability has been and is the sticking point in the relationship of arithmetic to geometry.
It is not only an intellectual problem, but it has been an extremely practical one in the history of science. For if we want to involve AB, CD in some calculation, there is no number to write! AB = ? × CD.
The problem was first realized by Pythagoras in the 6th century B.C. He discovered it by looking at a simple square.
The square drawn on the diagonal
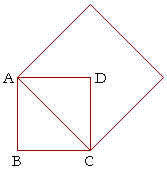
Let ABCD be a square, and on its diagonal AC, draw a square.
Problem 1.
a) What ratio has the square drawn on the diagonal AC to the square on
a) the side BC?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
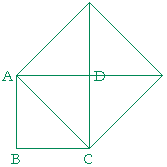
The square on the diagonal is twice the square on the side. For, we can see that the square on the diagonal AC is made up of four equal triangles, while the square on the side BC is made up of two of them.
b) Are the diagonal and side commensurable or incommensurable?
Incommensurable. The squares on them are in the ratio 2 : 1, and 2 is not a square number.
c) Explicitly, what ratio has the diagonal to the side?
Can you express it?
"Speechless"
The student should know that this discovery -- The diagonal and side of a square are incommensurable -- was a landmark in the history of mathematics. It drove home the distinction between geometry and arithmetic; between what is continuous and what is discrete; and, as we are about to see, it led to the invention of irrational numbers.
Pythagoras realized that we cannot say how the diagonal and side are related, and he referred to their ratio as "speechless." That has been called mathematics first logical scandal.
Nevertheless, knowledge of a square figure is still rational: The square drawn on the diagonal is twice the square on the side. This suggests that the fundamental magnitude is not length but area. Area --the figure itself -- is what is geometrically real.
The invention of irrational numbers
We have seen (Lesson 9) that if squares are in the same ratio as two square numbers, then their sides will have the same ratio as the square roots. Thus if CD were 1 meter, then we would like to say that AB is "Square root of 2" meters -- but there is no such rational number. For if there were, then again, AB, CD would have a common measure, which they do not.
If we insist, however, that there be a number to indicate the ratio AB : CD, then we keep the name "Square root of 2," and we call it an irrational number. Its numeral is 
. That is,
× = 2.
is that number which when multiplied by itself -- when squared -- is 2. "Square root of 2" is its name. It is not any whole number, any fraction, any mixed number or any decimal -- it is not any rational number. It is a pure creation.
For suppose were a rational number. Then we could express it as
| a fraction | m n |
in lowest terms. That is, suppose |
| m n |
· | m n |
= | m· m n· n |
= 2 |
| But that is impossible. Since | m n |
is in lowest terms, then m and n |
have no common divisors except 1. Therefore, m· m and n· n also have
| no common divisors. It will be impossible to reduce | m· m n· n |
and |
get 2
There is no rational number whose square is 2.
Naturally, we wonder, "How much is 
?" But we can only answer, "Well, it's almost 1.414." How would anyone know that? Because 1.414 squared is almost 2.
1.414 × 1.414 = 1.999396
We could come closer to 2 by approximating to more decimal places. But no decimal squared can ever be exactly 2. is irrational.
It was argued for many centuries whether "really" is a number. Mathematicians thought of as a convenient symbol, but as for its being a number, that was something else. Because again, if we ask, How much is it?. . . we cannot say.
In the following Topic, we will investigate the existence of irrational numbers.
In any event, is not the only irrational number. Let us illustrate this by asking:
The square roots of which numbers are rational?
Answer. Only the square roots of square numbers. Thus,
= 1 is rational.
, 
are irrational.
= 2 is rational.
, 
, 
, 
are irrational.
= 3 is rational.
And so on.
Problem 2. Say the name of each number.
| a) |
Square root of 3. | b) |
Square root of 5. | |
| c) |
Two. It's rational. | d)  |
Square root of 3/5. | |
e)  |
Three-fifths. | f) |
One. | |
Problem 3. Which of the following are rational numbers and which are irrational?
a)  |
Irrational. | b)  |
Rational. | |
c)  |
Rational. | d)  |
Irrational. | |
A common measure with 1
We have seen that every number has a ratio to 1. A rational number is to 1 in the same ratio as two natural numbers. That is, every rational number has a common measure with 1 (Topic 8). We can say, then, that an irrational number is a number that has no common measure with 1.
1 and are incommensurable.
Problem 4. What number is a common measure of each pair?
a) 1 and 5 1
| b) 1 and | 5 8 |
1 8 |
c) 1 and 2.617 .001
d) 1 and
None.
Problem 5. Why have irrational numbers been invented?
To express the ratios of incommensurable magnitudes.
Problem 6. The squares on the sides of triangle ABC are in the ratio 1 : 4 : 3. Express the ratio of each pair of sides as a ratio of numbers, whether rational or irrational.
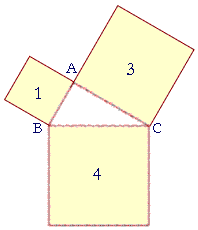
a) AB : BC =
1 :
2
b) BC : CA =
2 :
c) CA : AB =
:
1
| d) is approximately 1 |
5 7 |
, or | 12 7 |
. How could you know that? |
| 12 7 |
· | 12 7 |
= | 144 49 |
-- which is almost 3. |
e) Use that approximation to approximate the ratio of BC to CA as a
e) ratio of natural numbers.
| BC : CA = 2 : | 12 7 |
= 14 : 12 = 7 : 6 |
Problem 7. One square is four fifths of another.
a) Are the sides commensurable?
No. 4 and 5 are not both square
a) numbers.
b) Express the ratio of the sides as a ratio of numbers.
2 : 
c) Are the squares commensurable?
Yes. They are in the same ratio as natural numbers.
Next Topic: The existence of irrational numbers
www.proyectosalonhogar.com