33
THE EQUATION OF A
STRAIGHT LINE
The equation of the first degree
The graph of a first degree equation
The x- and y-intercepts of a graph
y = 2x + 4
This is called an equation of the first degree. It is called that because the highest exponent is 1.
A solution to that equation is any values of x and y that will make the equation -- that statement -- true. For example, the ordered pair (1, 6) is a solution. Because upon replacing x with 1 and y with 6,
6 = 2· 1 + 4
6 is equal to 2· 1 + 4.
Another solution is (0, 4). Because when x = 0 and y = 4, then
4 = 2· 0 + 4,
which again is true.
It's easy to find solutions. Simply let x have any value you please -- the equation then determines the value of y. For that reason, x is called the independent variable; y is called the dependent variable.
Problem 1. Find three solutions to the first degree equation y = x + 4.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
For example: (0, 4), (1, 5), (2, 6).
Problem 2. Which of the following ordered pairs solve this equation:
y = 3x − 4 ?
(0, −4) (1, 2) (1, −1) (2, −3)
(0, −4) and (1, −1). Because when x and y have those values, the equation is true.
The graph of a first degree equation
Consider the equation
y = 2x + 1.
Since there are two variables, x and y, then is it possible -- on the x-y plane -- to draw a "picture" of all the solutions to this equation?
First, to find a few solutions, complete this table. That is, calculate the value of y that corresponds to each value of x:
| x | y = 2x + 1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| −1 | −1 |
Now plot these as points on the plane:
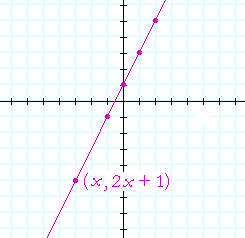
We see that all these solutions lie on a straight line. In fact, the x, y coordinates of every point on that line will solve the equation! Every coordinate pair is
(x, 2x + 1).
y = 2x + 1.
That line, therefore, is called the graph of the equation y = 2x + 1. And y = 2x + 1 is called the equation of that line.
Every first degree equation has as its graph a straight line. (We prove that in Topics in Precalculus .) For that reason, equations of the first degree -- where 1 is the highest exponent -- are called linear equations.
Problem 3.
a) An equation of the form y = ax + b has what graph?
A straight line. This is a linear equation.
b) An equation of the form Ax + By + C = 0 has what graph?
A straight line. This is a linear equation. The capital letters are a convention for indicating integer coefficients.
Problem 4. What characterizes a linear equation?
1 is the highest exponent.
Problem 5. Which of the following are linear equations?
| a) y = 4x − 5 | b) 2x − 3y + 8 = 0 | c) y = x² − 2x + 1 | ||
| d) 3x + 1 = 0 | e) y = 6x + x3 | f) y = 2 | ||
a), b), d), f).
Problem 6.
a) Name the coordinates of any three points on the line whose equation
a) is
y = 2x − 1.
(Pick any number for x; the equation will then determine the value
a) of y.)
For example, (0 −1), (1, 1), (−1, −3).
Problem 7.
a) Which of these ordered pairs solves the equation y = 5x − 6 ?
(You have to test each pair!)
(1, −2) (1, −1) (2, 3) (2, 4)
(1, −1) and (2, 4)
b) Which of those are points on the graph of y = 5x − 6 ?
(1, −1) and (2, 4)
Problem 8. True or false?
a) (−2, −3) is on the line whose equation is x + y = 5.
False.
b) (2, 3) is on the line whose equation is x + y = 5.
True.
Constants versus variables
A constant is a symbol whose value does not change.
The symbols '5' and '![]() ' are constants.
' are constants.
The beginning letters of the alphabet a, b, c, etc. are typically used to denote constants, while the letters x, y, z , are typically used to denote variables. For example, if we write
y = ax² + bx + c,
we mean that a, b, c are constants (i.e. fixed numbers), and that x and y are variables.
Problem 9. The constants a and b. Each of the following has the form y = ax + b. What number is a and what number is b?
| a) y = 2x + 3. | a = 2, b = 3. | b) y = x − 4. | a = 1, b = −4. | |
| c) y = −x + 1. | a = −1, b = 1. | d) y = 5x. | a = 5, b = 0. | |
| e) y = −2. | a = 0, b = −2. | f) y = −4x − 5. | a = −4, b = −5. | |
www.proyectosalonhogar.com
