Proof of the double-angle and half-angle formulas

Double-angle formulas

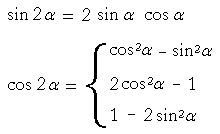
Proof

The double-angle formulas are proved from the sum formulas by putting β = .  We have

sin 2 = sin ( + )	=	sin cos + cos sin
	=	2 sin cos .
cos 2 = cos ( + )	=	cos cos − sin sin
cos 2	=	cos² − sin².   .  .  .  .  .  . (1)

This is the first of the three versions of cos 2.  To derive the second version, in line (1) use this Pythagorean identity:

sin² = 1 − cos².

Line (1) then becomes

cos 2	=	cos² − (1 − cos²)
	=	cos² − 1 + cos².
cos 2	=	2 cos² − 1.  .  .  .  .  .  .  .  .  .  (2)

To derive the third version, in line (1) use this Pythagorean identity:

cos² = 1 − sin².

We have

cos 2	=	1 − sin² − sin²;.
cos 2	=	1 − 2 sin².  .  .  .  .  .  .  .  .  .  (3)

These are the three forms of cos 2.

Half−angle formulas

Angle is half of the angle 2.  Therefore, in line (2), if we

put 2 = θ, then will equal

θ 2

:

cosine.

So, on exchanging sides and transposing 1, we have

2 cos²	θ 2	=	1 + cos θ
cos²	θ 2	=	½(1 + cos θ)
cos	θ 2	=	.

This is the half-angle formula for the cosine.  The sign ± will depend on the quadrant.  Again, whether we call the argument θ or does not matter.

Notice that this formula is labeled (2') -- "2-prime"; this is to remind us that we derived it from formula (2).

The formula for sin

θ 2

comes from putting 2 = θ in line (3).  On

transposing, line (3) becomes

	2 sin²	θ 2	=	1 − cos θ,
so that
	sin	θ 2	=	.

This is the half−angle formula for the sine.

Trigonometric identities

Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com