Note that the smallest side, 1, is opposite the smallest angle, 30°; while the largest side, 2, is opposite the largest angle, 90°. (Theorem 6). (For, 2 is larger than 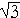 . And while 1:
. And while 1: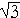 :2 more correctly corresponds to 30°-60°-90°, many find the sequence 1:2:
:2 more correctly corresponds to 30°-60°-90°, many find the sequence 1:2: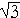 easier to remember.)
easier to remember.)
Problem 2. Evaluate cot 30° and cos 30°.
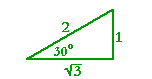
The cotangent is the ratio of the adjacent side to the opposite.
| Therefore, on inspecting the figure above, cot 30° = |
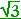
1 |
= 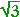 . . |
Or, more simply, cot 30° = tan 60°. Problem 1.
As for the cosine, it is the ratio of the adjacent side to the hypotenuse. Therefore,
| cos 30° = |
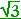
2 |
= ½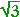 . . |
Before we come to the next Example, here is how we relate the sides and angles of a triangle:
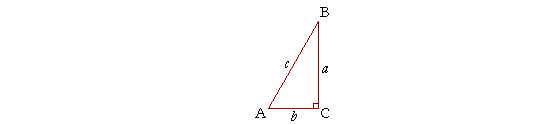
If an angle is labeled capital A, then the side opposite will be labeled small a. Similarly for angle B and side b, angle C and side c.
Example 3. Solve the right triangle ABC if angle A is 60°, and side c is 10 cm.
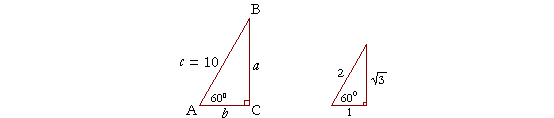
Solution. To solve a triangle means to know all three sides and all three angles. Since this is a right triangle and angle A is 60°, then the remaining angle B is its complement, 30°.
Now in every 30°-60°-90° triangle, the sides are in the ratio 1 : 2 : 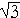 , as shown on the right. Whenever we know the ratios of the sides, we can solve the triangle by the method of similar figures.
, as shown on the right. Whenever we know the ratios of the sides, we can solve the triangle by the method of similar figures.
Thus, in triangle ABC, the side corresponding to 2 has been multiplied by 5. Therefore every side will be multiplied by 5. Side b will be 5 × 1, or simply 5 cm, and side a will be 5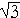 cm.
cm.
Alternatively, we could say that the side adjacent to 60° is always half of the hypotenuse. Therefore, side b will be 5 cm. Now, side b is the side that corresponds to 1. And it has been multiplied by 5. Therefore, side a must also be multiplied by 5. It will be 5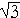 cm.
cm.
Whenever we know the ratio numbers, we use this method of similar figures to solve the triangle, and not the trigonometric Table.
(In Topic 8, we will solve right triangles the ratios of whose sides we do not know.)
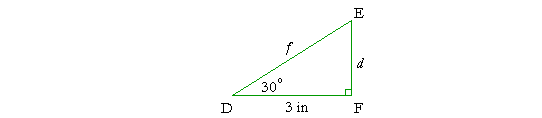
Problem 3. In the right triangle DEF, angle D is 30°, and side DF is 3 inches. How long are sides d and f ?
Problem 4. In the right triangle PQR, angle P is 30°, and side r is 1 cm. How long are sides p and q ?
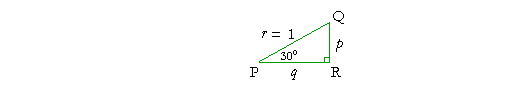

The side corresponding to 2 has been divided by 2. Therefore, each side must be divided by 2. Side p will be ½, and side q will be ½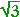 .
.
Problem 5. Solve the right triangle ABC if angle A is 60°, and the hypotenuse is 18.6 in.
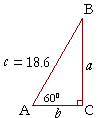
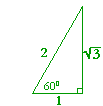
The side adjacent to 60° is always half of the hypotenuse -- therefore, side b is 9.3 in.
But this is the side that corresponds to 1. And it has been multiplied by 9.3. Therefore, side a will be multiplied by 9.3. It will be 9.3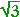 in.
in.
Problem 6. Inspect the values of 30°, 60°, and 45° -- that is, look at the two triangles -- and decide which of those angles satisfies each equation.
The proof
Here is the proof that in a 30°-60°-90° triangle the sides are in the ratio 1 : 2 : 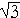 . It is based on the fact that a 30°-60°-90° triangle is half of an equilateral triangle.
. It is based on the fact that a 30°-60°-90° triangle is half of an equilateral triangle.
Draw the equilateral triangle ABC. Then each of its equal angles is 60°. (Theorems 3 and 9)
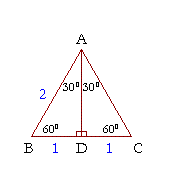
Draw the straight line AD bisecting the angle at A into two 30° angles.
Then AD is the perpendicular bisector of BC (Theorem 2). Triangle ABD therefore is a 30°-60°-90° triangle.
Now, since BD is equal to DC, then BD is half of BC.
This implies that BD is also half of AB, because AB is equal to BC. That is,
BD : AB = 1 : 2
From the Pythagorean theorem, we can find the third side AD: