19
INVERSE FUNCTIONS
The graph of an inverse function
THE INVERSE of a function undoes the action of that function.
![]()
Say, for example, that a function f acts on 5, producing f(5). Then if g is the inverse of f, then g acting on f(5) will bring back 5 !
g(f(5)) = 5
Actually, g must do that for all values in the domain of f. And f must do that for all values in the domain of g. Here is the definition:
Functions f(x) and g(x) are inverses of one another if:
f(g(x)) = x and g(f(x)) = x,
for all values in their respective domains.
Example 1. Let f(x) = x + 2, and g(x) = x − 2. Then they are inverses of one another. For g(x), which subtracts 2 from a number, is the inverse of adding 2: f(x).
Formally, according to the definition:
f(g(x)) = f(x − 2) = (x − 2) + 2 = x,
(f adds 2 to its argument), and
g(f(x)) = g(x + 2) = (x + 2) − 2 = x.
(g subtracts 2 from its argument
.)The definition is satisfied.
Problem 1. Let f(x) = x² and g(x) = x½. Show that they are inverses of one another. (The domain of f must be restricted to x ![]() 0.)
0.)
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
f(g(x)) = f(x½) = (x½)² = x,
and
g(f(x)) = g(x²) = (x²)½ = x.
Constructing the inverse
When we have a function y = f(x) -- for example
y = x²
-- then we can often "invert" the equation by solving for x. In this case,
![]()
x now appears as a function of y. Therefore on exchanging the variables,
![]()
| is the inverse function of y = x². |
(Taking the square root of a number is the inverse of squaring a number.)
Hence, to construct the inverse of a function y = f(x):
Solve for x, then exchange the variables.
Example 2. What function is the inverse of y = 3x + 4?
Solution. Exchange the sides of the equation, and solve for x:
| 3x + 4 | = | y | ||
| 3x | = | y − 4 | ||
| x | = | y − 4 3 | . | |
| Exchange the variables: | ||||
| y | = | x − 4 3 | . | |
That function is the inverse of y = 3x + 4.
Problem 2. What function is the inverse of y = 5x?
On solving for x:
| x | = | y 5 |
. | |
| Therefore on exchanging the variables: | ||||
| y | = | x 5 |
. | |
Clearly, dividing by 5 is the inverse of multiplying by 5.
Problem 3. a) Let y = f(x) = x − 4. Construct its inverse, g(x).
| x − 4 | = | y | |||
| implies: | |||||
| x | = | y + 4. | |||
| g(x) | = | x + 4. | |||
b) Prove that f(x) and g(x) are inverses.
f(g(x)) = f(x + 4) = (x + 4) − 4 = x,
and
g(f(x)) = g(x − 4) = (x − 4) + 4 = x.
Notation
The function I(x) = x is called the identity function. It always returns x.
As a notation for the inverse of a function f, we sometimes see f −1 ("f inverse"). "−1" is not an exponent. That notation is used because in the language of composition of functions, we can write:
f o f −1 = I
This is similar in form to the multiplication of numbers, a· a−1 = 1.
| * | * | * |
For the inverse trigonometric functions, see Topic 20 of Trigonometry.
The graph of an inverse function
The graph of the inverse of a function f(x) can be found as follows:
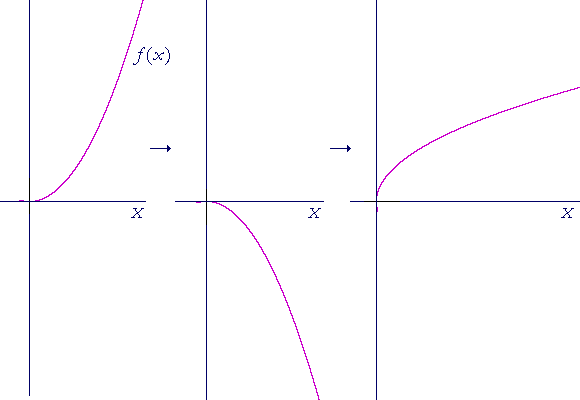
Reflect the graph about the x-axis, then rotate it 90° counterclockwise.
To see that in fact that is the graph of the inverse, consider the following:
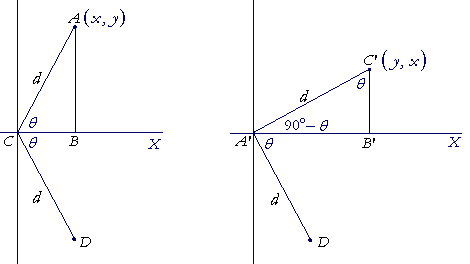
Let A be a point on the graph of f(x) whose coordinates are (x, y), and which is a distance d from the origin C; AC makes an angle θ with the x-axis; triangle ABC is right angled.
The figure on the left shows the reflection of A about the x-axis to the point D. The figure on the right shows the rotation 90° counterclockwise to the point C'. In that figure, C'A' makes an angle of 90° − θ with the x-axis. That is, in the right triangle A'B'C', angle C'A'B' is the complement of angle θ. Therefore the angle at C' is equal to θ.
But the angle at A is the complement of θ. Therefore the triangles ABC, A'B'C' are congruent (Angle-side-angle), and those sides are equal that are opposite the equal angles:
A'B' is equal to AB -- which is the y-coordinate .
B'C' is equal to BC -- which is the x-coordinate .
Therefore the coordinates of C' are (y, x).
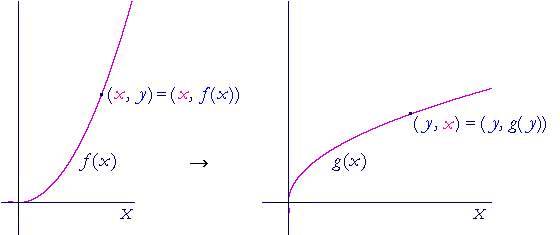
In other words, when each point (x, y) on f(x) is transformed into (y, x), then a graph of a functions g(x) results. And we claim that the graph of
g(x) is the graph of the inverse of f(x).
For, when g operates on its x-coordinate -- which is the y-coordinate of f -- it produces x:
g( y ) = x.
But y is f(x):
g( f(x)) = x.
And that is the definition of the inverse! The graph of g(x) is the graph of the inverse of f(x).
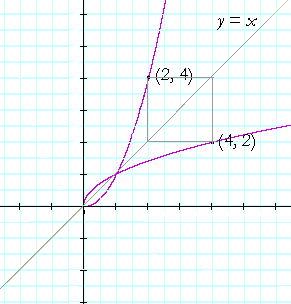
What is more, we can now see that the graphs of a function and its inverse are symmetrical with respect to the straight line y = x.
www.proyectosalonhogar.com
