Book I. Propositions 39 - 41

THE NEXT TWO PROPOSITIONS are partial converses of the previous two; they show that if equal triangles are on the same base or on equal bases, then they are in the same parallels.

PROPOSITION 39. THEOREM

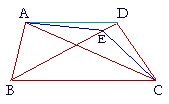
Equal triangles that are on the same base and on the same side of it, are in the same parallels.

Let triangles ABC, DBC be equal, and on the same base BC, and on the same side of it; then they will be in the same parallels.



Draw AD; then AD will be parallel to BC.

For if it is not, then through A draw AE parallel to BC, meeting
BD at E;	(I. 31)

and draw EC.

Then triangle ABC is equal to triangle EBC because they are on the same base BC and in the same parallels.	(I. 37)

But triangle ABC is equal to triangle DBC.	(Hypothesis)

Therefore triangle EBC is also equal to triangle DBC,	(Axiom 1)

the smaller to the larger; which is impossible.	(Axiom 5)

Therefore AE is not parallel to BC.

In the same manner we can prove that neither is any other straight line through A except AD;

therefore AD is parallel to BC.

Therefore, equal triangles that are on the same base etc. Q.E.D.

The next theorem, Proposition 40, is the partial converse of Proposition 38, and we shall leave the enunciation of it as an exercise; Problem 2.

Now any triangle is half of a parallelogram; half the area, that

is. That was implied in I. 37 and 38. The following theorem confirms it.

PROPOSITION 41. THEOREM

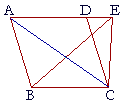
If a parallelogram and a triangle are on same base and in the same parallels, the parallelogram is double the triangle.

Let the parallelogram ABCD and the triangle EBC be on the same base BC, and in the same parallels AE, BC; then the parallelogram ABCD is double triangle EBC.



Draw AC.

Then the parallelogram ABCD is double triangle ABC, because the diagonal AC bisects the parallelogram.	(I. 34)

But triangle ABC is equal to triangle EBC, because they are on the same base BC, and in the same parallels AE, BC.	(I. 37)

Therefore parallelogram ABCD is also double triangle EBC.

Therefore, if a parallelogram etc. Q.E.D.

From this theorem we derive the arithmetical formula that the area of a triangle is one-half the measure of the base times the measure of the height: A = ½bh.

Transformation of areas

Euclid's next four propositions began a fascinating problem in geometrical knowledge, which is to construct a simple figure, such as a rectangle or a square, which will be equal in area to a given figure. Proposition I. 45 solves the problem of constructing a rectangle equal to any rectilinear figure; and Proposition II. 14 solves the problem of constructing a square equal to any rectilinear figure. But an unsolved problem was to "square the circle," that is, to construct a square equal to a given circle. Not until the 19th century was it proved that that construction, using straightedge and compass alone, is impossible. The Pythagoreans were the ones who initiated and solved all these problems relating to rectilinear areas, and we shall have more to say about them when we prove Pythagoras's theorem.

The next proposition solves the problem of constructing a "square."

Please "turn" the page and do some Problems.

Continue on to the next proposition.

Previous proposition

Table of Contents | Introduction | Home