THE SIDES AND ANGLES OF A TRIANGLE

Book I. Proposition 20

Here, finally, is Proposition 20. It depends on Proposition 18. To prove, in triangle ABC, that sides BA, AC are greater than side BC, on side AC we construct the isosceles triangle DAC.

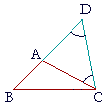
Since AC is equal to AD, then side BD -- which is BA, AD -- is equal to BA, AC. It is not difficult to see that angle DCB is greater than angle D, so that the opposite side BD is greater than opposite side BC.

But BD is equal to BA, AC. Therefore BA, AC are greater than BC.

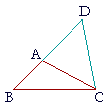
PROPOSITION 20. THEOREM

Any two sides of a triangle are together greater than the third side.

Let ABC be a triangle;
then any two sides of it taken together are greater than the remaining side; namely,

BA, AC are greater than BC;

AB, BC are greater than AC;

BC, CA are greater than AB.



Extend BA to D, making AD equal to AC, and draw DC.

Then, since CA is equal to AD,	(Construction)

angle ADC is equal to angle ACD.	(I. 5)

Now angle BCD is greater than angle ACD;	(Axiom 5)

therefore angle BCD is greater than the equal angle ADC.

In triangle DCB, then, angle DCB is greater than angle BDC;

and the greater angle is opposite the greater side;	(I. 19)

therefore,

side BD is greater than side BC.

But BD is equal to BA, AD together,

and AD is equal to AC;

therefore BD is equal to BA, AC together;

therefore BA, AC are greater than BC.

Similarly, we can prove that AB, BC are greater than CA, and BC, CA greater than AB.

Therefore, any two sides etc. Q.E.D.

Please "turn" the page and do some Problems.

Continue on to the next proposition.

Previous proposition

Table of Contents | Introduction | Home