STRAIGHT ANGLES, VERTICAL ANGLES

Book I. Propositions 13 and 14

WE KNOW THAT WHEN A STRAIGHT LINE that stands on another

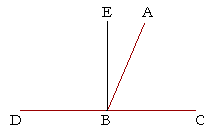
straight line makes the adjacent angles equal, then we have two right angles. But it should be obvious that when any straight line stands on another, then the adjacent angles ABC, ABD are together equal to two right angles. That is the next proposition.

(The proof will show that the two right angles CBE, EBD
are equal to the three angles CBA, ABE, EBD;
but angles CBA, ABD are also equal to those three angles;
therefore CBA, ABD are equal to the two right angles.)

PROPOSITION 13. THEOREM

When a straight line that stands on another straight line makes two angles, either it makes two right angles, or it makes angles that together are equal to two right angles.

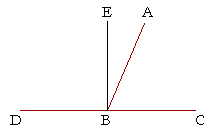
Let the straight line AB stand on the straight line CD and make the

two angles CBA, ABD;

then either angles CBA, ABD are two right angles, or together they are

equal to two right angles.


For if angle CBA is equal to angle ABD, then they are two right
angles.	(Definition 3)

But if they are not equal, then draw BE from the point B at right angles

to CD;	(I. 11)

therefore angles CBE, EBD are two right angles.

Now, since angles

CBA, ABE are equal to angle CBE,

to each of these add the right angle EBD;

therefore the three angles

CBA, ABE, EBD are equal to angles CBE, EBD.	(Axiom 2)


And, since angles

ABE, EBD are equal to angle ABD,

to each of these add angle CBA;

therefore the three angles

CBA, ABE, EBD are equal to angles CBA, ABD.	(Axiom 2)

But we have shown that angles CBE, EBD are equal to those same three angles;

and things that are equal to the same thing are equal to one another;
(Axiom 1)
therefore angles

CBA, ABD are equal to angles CBE, EBD.

But CBE, EBD are two right angles;

therefore angles CBA, ABD are together equal to two right angles.

Therefore, when a straight line that stands on another straight line etc. Q.E.D.

Corollary 1. When two straight lines intersect one another, the four angles they make are together equal to four right angles.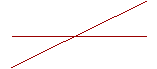

Corollary 2. Therefore when any number of straight lines intersect at one point, all the angles they make are together equal to four right angles.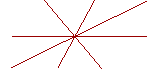

The hypothesis of Proposition 13 is that the straight line which stands on the other makes two angles. But how could it not make two angles? If it stood at the extremity of the line. In that case, it would make only one angle.

When it does not stand at the extremity, however, then the angles formed are equal to two right angles. Conversely -- if angles

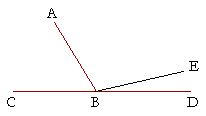
ABC, ABD together are equal to two right angles, then BD is in a straight line with CB!

This is Proposition 14. But there is no previous proposition or definition that gives a criterion for two straight lines being in a straight line. This proposition is the criterion. Therefore, it can be proved only by the indirect method.

Thus, if we assume that BD is not in a straight line with CB, then we may assume that BE is, because the straight line CB may be extended in a straight line. But this leads to the conclusion that angle ABE is equal to angle ABD, the smaller to the larger; which is absurd. (Can you show that?) It follows, then, that BD is the only straight line that is in a straight line with CB.

PROPOSITION 14. THEOREM

If two straight lines are on opposite sides of a given straight line, and, meeting at one point of that line they make the adjacent angles equal to two right angles, then the two straight lines are in a straight line with one another.

Let two straight lines CB, BD be on opposite sides of the straight line AF, meeting at the point B, and let the adjacent angles ABC, ABD be equal to two right angles; then BD will be in a straight line with CB.


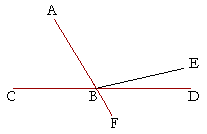For if BD is not in a straight line with CB, let BE be in a straight line with CB.

Then, since the straight line AB stands on the (supposed) straight line CBE,

it makes the adjacent angles ABC, ABE equal to two right angles.	(I. 13)


But angles ABC, ABD are also equal to two right angles.	(Hypothesis)

Therefore angles ABC, ABE are equal to angles ABC, ABD.
(Postulate 4 and Axiom 1)

From each pair subtract angle ABC;

then the remaining angle ABE is equal to the remaining angle ABD,
(Axiom 3)
the smaller to the larger -- which is absurd.

Therefore BE is not in a straight line with CB.

In the same manner we can prove that neither is any other straight line except BD.

Therefore, if two straight lines etc. Q.E.D.

Straight angles

An angle in plane geometry is strictly less than two right angles.

We do not think of angles ABC, CBD together as one angle. The angle we call angle ABD is the obtuse angle ABD, which is less than two right angles.

If CD is a straight line, then, and AB meets it, we would not

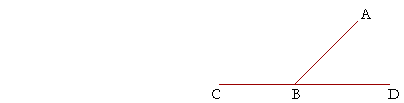
normally call CBD an "angle;" however it has become customary to call it a straight angle.

A straight angle is equal to two adjacent angles
that together are equal to two right angles.

When two angles are equal to two right angles -- to a straight angle -- we say that they are supplements of one another, or that they are supplementary angles. Thus angle ABC above is the supplement of angle ABD, and vice-versa. It will be left to Problem 5 to prove the simple theorem:

Angles that are supplements of the same angle are equal to one another.

Please "turn" the page and do some Problems.

Continue on to the next proposition.

Previous proposition

Table of Contents | Introduction | Home