EQUALITY OF NON-CONGRUENT AREAS

Book I. Propositions 35 and 36

WE SPEAK OF PARALLELOGRAMS that are "in the same parallels."

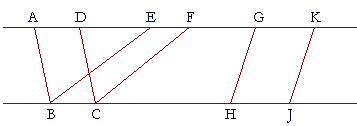
Thus if AK, BJ are parallel, then the parallelograms ABCD, GHJK are in the same parallels.

Further, two parallelograms may be "on the same base and in the same parallels," as are ABCD and EBCF. They are on the same base BC, and in the same parallels AF, BC.

Equality of non-congruent areas

If the theorem about the three angles of a triangle was the first triumph of the theory of parallel lines (I. 32), then the following theorem is the second, because it establishes how we can know when areas that are not congruent are equal.

The theorem proves that parallelograms on the same base and in the same parallels are equal.

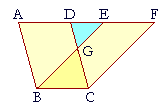
Parallelograms ABCD, EBCF are on the same base BC and in the same parallels AF, BC. We can then show that triangles ABE, FDC are equal (S.A.S). On subtracting DGE from those triangles and then adding GBC, we can see that the resulting parallelograms are equal!

PROPOSITION 35. THEOREM

Parallelograms on the same base and in the same parallels are equal.

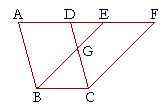
Let ABCD, EBCF be parallelograms on the same base BC and in the same parallels AF, BC; then ABCD and EBCF are equal areas.



For, since ABCD is a parallelogram,

AD is equal to BC.	(I. 34)

For the same reason,

EF is equal to BC, so that AD is equal to EF.	(Axiom 1)

Therefore if we add DE to each,

the whole AE is equal to the whole DF.	(Axiom 2)

Now, AB is equal to DC;	(I. 34)

therefore the two sides EA, AB of triangle EAB

are equal respectively to the two sides FD, DC of triangle FDC;

and the exterior angle FDC is equal to the interior angle EAB;	(I. 29)

therefore triangle EAB is equal to triangle FDC.	(S.A.S.)



Subtract triangle DGE from each one;

then the quadrilateral ABGD which remains is equal to the quadrilateral FEGC which remains.	(Axiom 3)

Add triangle GBC to each quadrilateral;

then the whole parallelogram ABCD is equal to the whole parallelogram EBCF.	(Axiom 2)

Therefore, parallelograms on the same base etc. Q.E.D.

PROPOSITION 36. THEOREM

Parallelograms on equal bases and in the same parallels are equal.

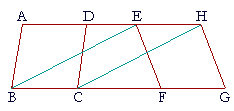
Let ABCD, EFGH be parallelograms on equal bases BC, FG, and in the same parallels AH, BG; then ABCD is equal to EFGH.


Draw BE, CH.

Then, since BC is equal to FG,	(Hypothesis)

and FG equal to EH,	(I. 34)

BC is equal to EH;	(Axiom 1)

and they are parallel,

and the straight lines BE, CH join their extremities on the same side.

But straight lines which join the extremities on the same side of two equal and parallel straight lines, are themselves equal and parallel.	(I. 33)

Therefore BE, CH are equal and parallel.

Therefore EBCH is a parallelogram.	(Definition 14)

And it is equal to ABCD, because they are on the same base BC, and in the same parallels BC, AH.	(I. 35)


For the same reason, EBCH is equal to EFGH,

because they are on the same base EH.

Therefore the parallelogram ABCD is equal to the parallelogram EFGH.	(Axiom 1)

Therefore, parallelograms on equal bases etc. Q.E.D.

From these theorems we derive the arithmetical formula that the area of a parallelogram is equal to the measure of the base times the measure of the height: A = b × h. For, the height of a parallelogram is the distance between the parallels.

Please "turn" the page and do some Problems.

Continue on to the next proposition.

Previous proposition

Table of Contents | Introduction | Home