|
|
MÓDULO INSTRUCCIONAL DE CURRÍCULO
Titulo: Algebra
Grado: Noveno
Módulo Núm. 2
TABLA DE CONTENDO
Pre- Prueba
Instrumentos de Navegación
Introducción
Objetivos
Materiales y Equipo
Lección # 1 Operaciones básicas con matrices
Multiplicación de matrices
Propiedades de la multiplicación de matrices
Producto de una matriz escalar
Lección # 2 Sistema de Ecuaciones
Método Matricial
Matriz Ampliada
Lección # 3 Sistema de Ecuaciones Lineales
Método Gráfico
Método Sustitución
Método Igualación
Método Eliminación
Respuestas Ejercicios: Lección#1,Lección #2, Lección #3
Post- Prueba
Apéndice
Referencias
PRE- PRUEBA
Escoge la mejor contestación.
1) El objeto que representa las conexiones se conocen como:
a) elementos
b) matriz
c) filas
d) columnas
2) El conjunto ordenado de elementos de una matriz, se conoce como:
a) columna
b) elementos
c) matriz
d) filas
3) Los conjuntos matemáticos de una matriz, se conoce:
a) elementos
b) filas
c) columnas
d) matriz
4) Un matriz cuadrada, tiene una dimensión de :
a) 2 x 2
b) 3 x 3
c) 4x 4
d) 1 x 1
5) El tamaño de la matriz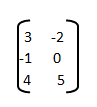 
a) 2 x 3
b) 3 x 2
c) 6 x 1
d) 1 x 6
6) En la matriz A =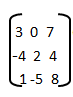 
el elemento a32 es:
a) 4
b) -4
c) 8
d) -5
7) El tamaño de la matriz 
es:
a) 1 x 4
b) 4 x 1
c) 4 x 4
d) 1 x1
8) El resultado de la multiplicación de las matric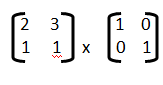es 
es:
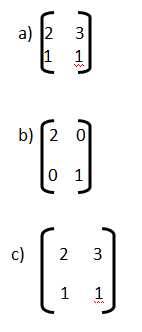
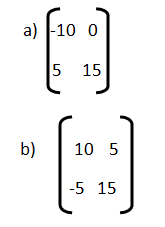
9) El producto polar de la siguiente matriz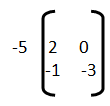 
es:
10) La expresión general de una ecuación lineal es ax + by = c, la letra a es:
a) coeficiente
b) término constante
c) variable de la ecuación lineal
d) solución
11) La letra c en ax+ bx = c, representa:
a) término constante
b) coeficiente
c) solución
d) elemento
12) La solución del sistema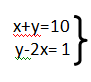 
es
a) x= 7, y=3
b) x=2, y=8
c) x=3, y=7
d) x=5, y=5
13) Resuelve, usando el método de sustitución,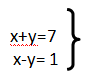 
a) x=4,y=3
b) x=3, y=4
c) x=-3, y=4
d) x= -4, y=3
14) Si 2x-3y=11, 3x+15=0, entonces y =_______.
a) -7
b) -5
c) 1/3
d) 5
15) Si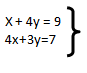 
entonces 5x + 7y = ________.
a) 8
b) 9
c) 16
d)18
16) El valor de x que satisface la siguiente ecuación ,12p -79=17, es:
a) -8
b) 8
c) 62
d) 96
INSTRUMENTOS DE NAVEGACION
Salir al comienzo del módulo- |
 |
|
Ir a la página anterior- |
 |
|
Ir a la página siguiente- |
 |
|
INSTRUMENTOS DE NAVEGACION
* La presentación inicia con el material teórico con los conceptos generales.
* Se recomienda que tengas acceso a Internet mientras trabajas la presentación.
* Siempre que se te presente la siguiente figura:
Ir a la página anterior- |
|
|
Ir a la página siguiente- |
|
puedes presionarla para navegar adecuadamente a través de toda la presentación.
* Luego de leer el material que sirve de introducción, podrás establecer enlaces que demuestran de forma dinámica los conceptos teóricos.
INTRODUCCION
Las matrices son una herramienta importante en la representación de ideas matemáticas. Sus aplicaciones alcanzan todas las ramas de las matemáticas y ciencias. El concepto de matriz es tan importante que existe toda una rama de las matemáticas que trata exclusivamente el estudio de las matrices, esta se conoce como el álgebra lineal. Veremos en este módulo los conceptos generales de matrices y las aplicaciones a la solución del sistema de ecuaciones lineales.
OBJETIVOS
Al finalizar el módulo el estudiante podrá:
n realizar la multiplicación de matrices
n aplicar las propiedades en la multiplicación de las matrices
n representación de matrices de un sistema de ecuaciones lineales
MATERIALES Y EQUIPO NECESARIO
Modulo Instruccional en “PowerPoint”
Laptop
Papel Cuadriculado
Lápices a colores
Regla
LECCION # 1
MATRIZ
En matemáticas, una matriz es una tabla bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse. Las matrices se utilizan para describir sistemas de ecuaciones lineales, realizar un seguimiento de los coeficientes de una aplicación lineal y registrar los datos que dependen de varios parámetros. Las matrices se describen en el campo de la teoría de matrices. Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
Ejemplo:
Dada la matriz: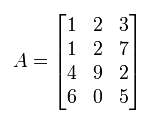 
que es una matriz 4x3. El elemento
La matriz
es una matriz 1× 9, o un vector fila con 9 elementos.
OPERACIONES BASICAS DE LAS MATRICES
A. MULTIPLICACIÓN DE MATRICES
Dos matrices A y B son multiplicables en el número de columnas de A coincide con el número de filas de B.
n M m x n X M n x p = M m x p
El elemento de la matriz producto se obtiene multiplicando cada elemento de la fila de la matriz A por cada elemento de la matriz B y sumándolos.
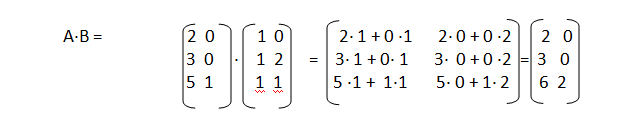
B. PROPIEDADES DE LA MULTIPLICACIÓN DE MATRICES
n PROPIEDAD ASOCIATIVA
A · ( B · C ) = (A·B) ·C
n ELEMENTO NEUTRO
A· I = A ,donde el elemento identidad (I) del mismo orden que la matriz A
n DISTRIBUTIVA DEL PRODUCTO RESPECTO DE LA SUMA
A· ( B + C) = A· B + A ·C
C. PRODUCTO DE UN MATRIZ ESCALAR
n En matemática la multiplicación o producto de matrices es la operación de multiplicación que se efectúa entre las matrices, o bien entre una matriz y un escalar. Dada una matriz A mxn = (a I j ) mxn y un número real K, el producto de k · A es la matriz de orden mxn que se obtiene al multiplicar cada elemento de A por k.
k · A mxn = ( k a I j) m x n
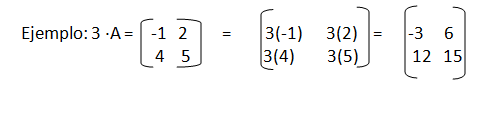
Ejercicio #1: Resuelve el siguiente ejercicio.
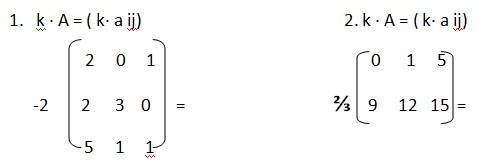
LECCION # 2
SISTEMA DE ECUACIONES LINEALES METODO MATRICIAL
Cualquier sistema de ecuaciones lineales puede escribirse siempre en forma matricial de la siguiente forma:
A· X = B donde A es la matriz de los coeficientes y B la matriz de los términos independientes
El sistema de ecuaciones lineales:
3x + 2y – z = 4
5x + y -3z = -6
x + 7z = 1
se expresa matricalmente:
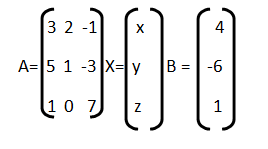
Ejercicio #2
a) Expresa la siguiente ecuación lineal en forma matricial.
x – 2y = 1
-x + 3y = 2
Forma Matricial:
LECCION # 3
A. SISTEMA DE ECUACIONES LINEALES
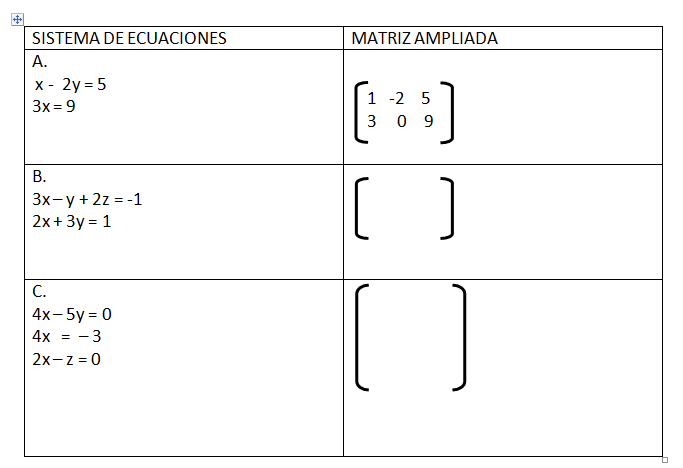
1. MATRIZ AMPLIADA
En la ecuación lineal:
ax + by + cz + . . . + dw = e,
los números a, b, . . ., d se llaman los coeficientes de la ecuación, y es el término constante o sencillamente el lado derecho.
La matriz ampliada de un sistema de ecuaciones lineales es la matriz cuyos renglones (o filas) son los coeficientes de las ecuaciones incluyendo los lados derechos:
Ejercicio #3.Completa la siguiente tabla.
1. ECUACIONES LINEALES
Una ecuación de primer grado con una incógnita es una ecuación algebraica que tiene una sola incógnita con exponente de 1. L solución de una ecuación lineal con dos incógnitas (variables) es el par de valores que verifican la igualdad. Las ecuaciones lineales tienen infinitas soluciones.
La expresión general de una ecuación lineal es:
Existen diferentes métodos para resolver sistemas de ecuaciones lineales, estos son: igualación, sustitución, eliminación, y gráfico.
A. Método gráfico
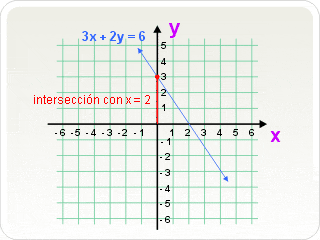
Una ecuación lineal es la fórmula algebraica que corresponde a la representación gráfica de una línea y sigue la referencia de:
y= mx + b
donde "m" es la pendiente de la recta y "b" es el punto donde la recta intersecta al eje de las "y".
por ejemplo: 3x + 2y = 6 , pendiente = m = 3, su gráfica es la siguiente:
Para dibujar la gráfica de una ecuación lineal con dos variables, el proceso es el siguiente:
a) resolver la ecuación para y
b) hacer una tabla de pares ordenados, se asignan valores para x y luego se resuelve para y
c) localizar los p untos en el plano cartesiano
d) unir los puntos
Ejemplo: Dibuja la gráfica de x + y = 4
Despejamos para y :
y = -x + 4
TABLA DE VALORES.
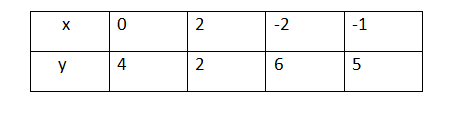
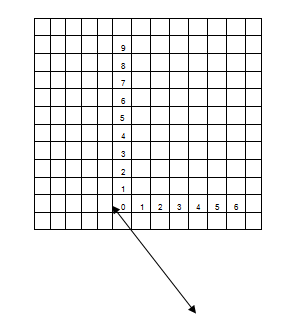
Ejercicio#2. Di buja la gráfica de la siguiente ecuación lineal.
a) y = -2x
Otra forma de resolver una ecuación lineal:
1. Graficar la ecuación lineal 4x – 3y = 12, encontrando la intersección con los ejes coordenadas.
Paso #1. Convertiremos la ecuación en la forma Ax +By +C = 0
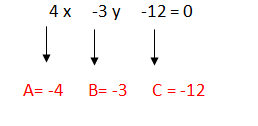
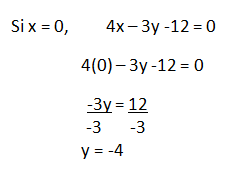
El punto (0, -4) es una solución, en un punto perteneciente a la línea recta.
Paso #3. Hacemos y = 0 y despejamos X de la ecuación.
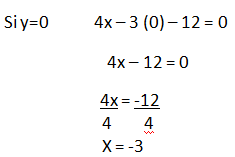
El punto (3,0) es una solución, en un punto perteneciente a la línea recta.
Paso #4: Graficar la ecuación 4x – 3y = 12
Localizamos los puntos (0,-4) y (3,0) en el plano cartesiano y trazamos la recta. Realiza la gráfica.
B. Método Sustitución
Para resolver un sistema de ecuaciones por el método de sustitución:
a) se despeja una de las incógnitas en una de las ecuaciones
b) se sustituye la expresión obtenida en la otra ecuación.
c) se resuelve la ecuación de una incógnita resultante.
d) Se calcula el valor de la otra incógnita en cualquiera de las ecuaciones.
Ejemplo:
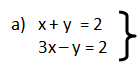
Procesos:
1) se despeja una de las incógnitas en una de las ecuaciones, usaremos la primera:
x = 2-y
2) se sustituye la expresión obtenida en la otra ecuación.
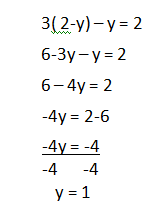
3) se calcula la otra incógnita en la ecuación despejada.
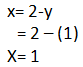
4) solución: (1, 1)
Ejemplo: Resuelve por el método de sustitución.
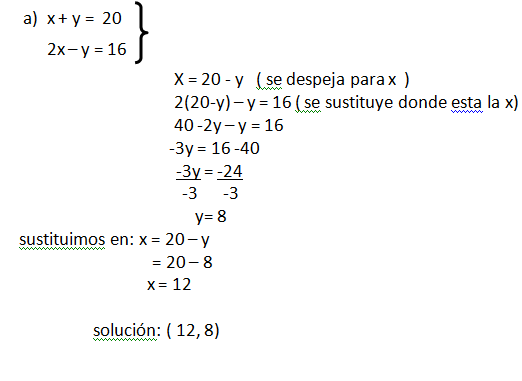
C. Método de Igualación
Para resolver un sistema de ecuaciones por el método de igualación:
a) se despeja la misma incógnita o variables en ambas ecuaciones.
b) Se igualan las expresiones obtenidas
c) Se resuelve la ecuación resultante
d) Se calcula el valor de la otra incógnita, sustituyendo en cualquiera de las ecuaciones , (este procedimiento es mas sencillo si usas un a de las ecuación es despejadas)
Ejemplo:
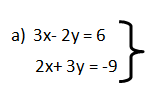
Procesos:
a) se despeja la misma incógnita en ambas ecuaciones (por ejemplo x)
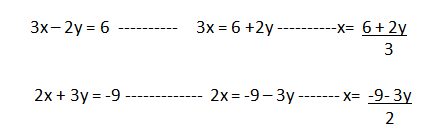
b) se igualan las expresiones obtenidas; y se resuelve la ecuación resultante.
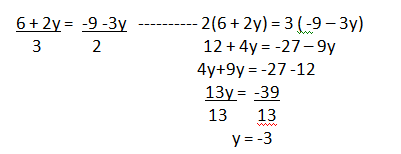
c) se calcula el valor de la incógnita, sustituyendo en cualquiera de las ecuaciones,(aquí, usamos la primera que despejamos).
D. Método de Eliminación
Para resolver un sistema de ecuaciones por el método de eliminación:
a) se igualan los coeficientes de una incógnita, excepto el signo, y se elige un múltiplo común de ambos coeficientes.
b) Se suma n ose restan las dos ecuaciones del sistema resultante, para reducir el sistema a una ecuación sencilla.
c) Se resuelve la ecuación de una incógnita resultante.
d) Se calcula el valor de la otra incógnita, sustituyen do en una de las ecuaciones del sistema.
d) se calcula el valor de la otra incógnita, sustituyendo en una de las ecuaciones
del sistema.
2x + y = 5 ------- 2(3) + y = 5
6 + y = 5
y = 5 -6
y = -1
Solución : ( 3,1)
Ejemplo: Resuelve por el método de eliminación.
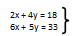
a) multiplicamos por -3 los dos miembros de la primera ecuación.
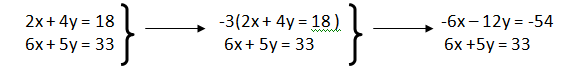
b) se suman o se restan las ecuaciones
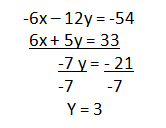
c) se calcula el valor de la otra incógnita
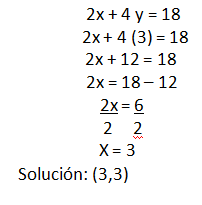
LECCION #3 Sistema de Ecuaciones Lineales
Ejercicios para resolver
EJERCICIOS
1. Resuelve las siguientes ecuaciones lineales por el método de sustitución.
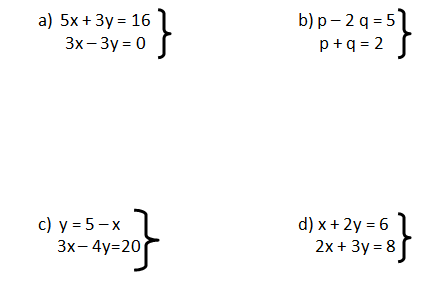
2. Resuelve las siguientes ecuaciones lineales por el método de igualación.
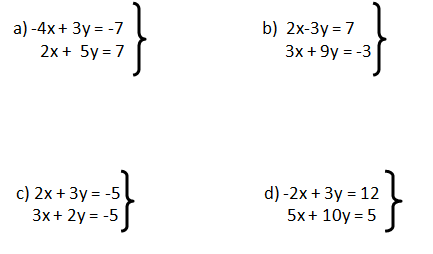
3) Resuelve las siguientes ecuaciones por el método de eliminación.
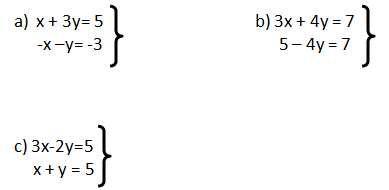
Respuestas a los ejercicios.
LECCION #1
Ejercicio #1
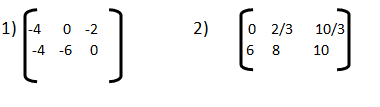
LECCION #2
Ejercicio #2
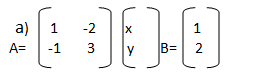
LECCION #3 .Sistemas de Ecuaciones Lineales. Respuestas a los ejercicios.
1. Método Sustitución
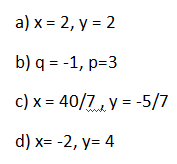
2. Método Igualación
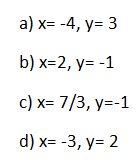
3. Método Eliminación
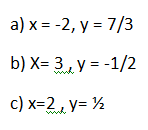
POS - PRUEBA
Escoge la mejor contestación.
1) El objeto que representa las conexiones se conocen como:
a) elementos
b) matriz
c) filas
d) columnas
2) El conjunto ordenado de elementos de una matriz, se conoce:
a. columna
b. elementos
c. matriz
d. filas
3) Los conjuntos matemáticos de una matriz, se conoce:
a. elementos
b. filas
c. columnas
d. matriz
4) Un matriz cuadrada, tiene una dimensión de :
a. 2 x 2
b. 3 x 3
c. 4x 4
d. 1 x 1
5) El resultado de la multiplicación de las matric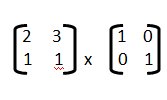es 
es
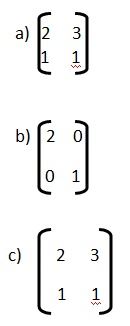
6) El producto polar de la siguiente matriz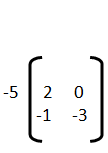 
es
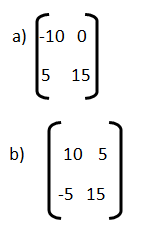
7) El tamaño de la matriz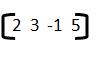 
es
a) 1 x 4
b) 4 x 1
c) 4 x 4
d) 1 x1
8) El resultado de la multiplicación de las matric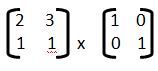es 
es
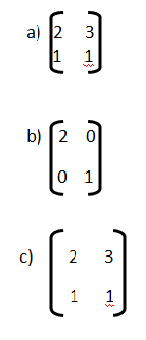
9) El producto polar de la siguiente matriz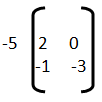 
es
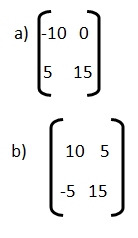
10) La expresión general de una ecuación lineal es ax + by = c, la letra a es:
a) coeficiente
b) término constante
c) variable de la ecuación lineal
d) solución
11) La letra c en ax+ bx = c, representa:
a) término constante
b) coeficiente
c) solución
d) elemento
12) La solución del sistema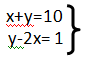 
es
a) x= 7, y=3
b) x=2, y=8
c) x=3, y=7
d) x=5, y=5
13) Resuelve, usando el método de sustitución,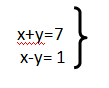 
a) x=4, y=3
b) x=3, y=4
c) x=-3, y=4
d) x= -4, y=3
14) Si 2x-3y=11, 3x+15=0, entonces y =_______.
a) -7
b)-5
c)1/3
d)5
15) Si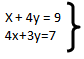 
entonces 5x + 7y = ________.
16) El valor de x que satisface la siguiente ecuación ,12p -79=17, es:
a) -8
b) 8
c) 62
d) 96
APENDICE
Respuesta a la Pre y Pos- Prueba
1) b
2) b
3) a
4) c
5) b
6) a
7) a
8) b
9) a
10) a
11) a
12) a
13) a
14) a
15) c
16) b
|