|
|

Titulo: Numeración y Operación

Módulo Núm. 1
Grado 9
Lección # 1 Matriz Matriz Cuadrada Transpuesta de una matriz Matriz Identidad Matriz Triangular Superior Matriz Triangular Inferior Matriz Triangular Ejercicios: Lección #1 Lección # 2 Operaciones Básicas Suma de Matrices Resta de Matrices Multiplicación de Matrices Producto Escalar
INTRODUCCIÓN
Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, ecuaciones diferenciales y de las derivadas parciales. Además, las matrices aparecen en forma natural en geometría, estadísticas, física, etc. En este módulo, entenderás los procesos y el desarrollo de las propiedades de suma y resta de matrices, analizar las mismas y resolver problemas. Objetivos: · Definir el concepto de matriz · Definir los conceptos de matrices cuadradas, matriz identidad, matriz transpuesta, matriz inversa, vectores, fila, columna y matrices triangulares. · Definir las operaciones entre matrices · Resolver ejercicios usando los procesos u operaciones de matrices
Materiales y equipos Necesarios: LECCION #1
MATRIZ Una matriz es un arreglo rectangular de números. Los números que forman la matriz se llaman entradas o elementos y se escriben dentro de corchetas. Las matrices se identifican con letras mayúsculas. Las líneas horizontales de números se conocen como filas y las verticales como columnas.
El número de filas por el número de columnas de una matriz se le llama el orden o tamaño de la matriz.
Una matriz que tiene n filas y n columnas, se llama matriz cuadrada de orden n. Los vectores fila de la matriz A están dados por
Similarmente, los vectores columna de la matriz A están dados por
La anterior matriz se puede expresar como A = ( aij)mxn , en donde aij representa el elemento de la matriz que esta en la fila i y en la columna j. A es una matriz cuadrada de orden 3, en donde a11= 0.6, a12=3, a21 = -2 A22= 0, a23= 1, a31 = 8, a32 = ⅓ y a33= 0 En una matriz cuadrad Amxn, los elementos { a11 , a22 ,…, ann } forman la diagonal principal de la matriz.
MATRIZ CUADRADA
Una matriz cuadrada es la que tiene el mismo número de filas que de columnas. Se dice que una matriz cuadrada n x n es de orden n y se denomina matriz n-cuadrada. ejemplo:
Entonces, A y B son matrices cuadradas de orden 3x 2, y 2x2 respectivamente. TRANSPUESTA DE UNA MATRIZ
Definición: Sea Amxn una matriz. La matriz transpuesta de A, es la matriz Bnxm definida por bji = aij para j = 1,…,n y i = 1,…,m
La transpuesta de A se denota por AT. Es decir que las filas de A pasan a ser las correspondientes columnas de AT.
Ejemplo:
a. Propiedades para la transpuesta de una matriz 1) ( AT) T = A 2) ( Ka)T = k AT , k escalar 3) (A + B)T = AT + B T 4) ( AB)T = BT AT Siempre y cuando las operaciones indicadas se pueden realizar.
MATRIZ IDENTIDAD
La matriz identidad de orden n, denotada por In es la matriz cuadrada nxn definida por
Es decir la matriz identidad, tiene “unos” en la diagonal y ceros fuera de la diagonal.
MATRIZ TRIANGULAR SUPERIOR
Una matriz cuadrada A = (aij ) es una matriz triangular superior o simplemente una matriz triangular, si todas las entradas bajo la diagonal principal son iguales a cero. Así pues, las matrices son matrices triangulares superiores de órdenes 2, 3 y 4. Sean A= (aij) una matriz cuadrada. A es una matriz triangular superior si: aij = o para i > j Es decir, todos los elementos por debajo de la diagonal principal son iguales a cero.
Ejemplo: A=
MATRIZ TRIANGULAR INFERIOR
Sea A= (aij) una matriz cuadrada. A es una matriz triangular inferior si Aij= 0 para i < j Es decir, todos los elementos por encima de la diagonal principal son iguales a cero.
Ejemplo: A =
EJERCICIOS: LECCION #1
1) Dar el tamaño de cada una de las siguientes matrices.
2) Dada la siguiente matriz
a) escribir los vectores fila de la matriz b) escribir los vectores columna de la matriz
3) Dadas las matrices A =
a) A + B b) A – B c) 4 A d) -3B e) 3A - 2B f) 2A + 4B
RESPUESTAS EJERCICIOS: LECCION #1
1) a) 2 x 3 b) 1 x 4 c) 4 x 1
LECCION #2 OPERACIONES BASICAS CON MATRICES
n SUMA DE MATRICES Para poder sumar matrices deben tener el mismo número de filas y columnas. Es decir, si una matriz es de orden 3x2 y otra 3x3, no se pueden sumar. Esto es así, ya que se suman los términos que ocupan el mismo lugar en las matrices. Sean las matrices A = ( a ij) mxn y B = (bij) mxn entonces la suma de A y B es la mariz (A+B) = ( aij + bij) mxn ; i = 1,…,m ; j + 1,…,n Es decir, para sumar dos matrices, estas deben tener el mismo tamaño y se procede a sumar los elementos correspondientes. Ejemplos 1:
Ejemplo 2:
RESTA DE MATRICES Para poder restar matrices están deben tener el mismo número de filas y de columnas. Se restarán los términos que ocupan el mismo lugar de matrices. Sean A y B dos matrices del mismo tamaño. Entonces A – B = A + (-B)
Ejemplo 1.
Ejemplo 2.
MULTIPLICACION DE MATRICES
Para poder multiplicar dos matrices, la primera debe tener el mismo número de columnas y filas que la segunda. La matriz resultante del producto quedará con el mismo número de filas de la primera y con el mismo número de columnas de la segunda. Ejemplo:
Ejemplo: Dadas las matrices A =
a) AB b) BA
Solución:
a) A(3x2) y B (2x3) . Número de columnas de A= Número de filas de B= 2, por lo tanto el producto de AB esta definido, y AB es una matriz de tamaño 3x3.
b) B(2x3) A(3x2) . Número de columnas de B= número de filas d A=3, por lo tanto el producto BA está definido y BA es una matriz de tamaño 2x2.
PRODUCTO POR UN ESCALAR
El producto por un escalar k por la matriz A, escrito k·A , o simplemente kA, es la matriz obtenida multiplicando cada entrada de A por k. Dada una matriz A = (aij) mxn y k un escalar, entonces el producto kA es la matriz kA = (kaij)mxn ; i=1,…,m ; j=1…,n
por ejemplo:
EJERCICIOS LECCION #2
1. Menciona las columnas, filas y tipo de matriz en los siguientes ejercicios.
2. Hallar la suma de las siguientes matrices.
3. Hallar la resta del siguiente ejercicio.
4. Hallar la resta del siguiente ejercicio de matriz.
5. Hallar la multiplicación de matrices, en el siguiente ejercicio.
6. Hallar la multiplicación de matrices en el siguiente ejercicio.
7. Resuelve la siguiente matriz por el proceso del producto por un escalar.
8. Realiza la suma de las siguientes matrices:
9. Realiza la resta de las siguientes matrices.
10. Realiza la multiplicación de las siguientes matrices.
11. Encuentra la multiplicación escalar:
12. Resuelve el siguiente ejercicio verbal:
Pedro invirtió $10,000 parte al 6% de interés anual y el resto al 12% anual. ¿Cuánto debe invertir a cada por ciento de manera que obtenga el 8% de interés anual? Resuelve usando matrices.
RESPUESTAS EJERCICIOS: LECCION # 2
1) FILAS A: ( 2,3,5,6) B: ( 6,5,0,-9)
Pos – Prueba
I. Escoge la mejor contestación. 1) El tamaño de la matriz [2 3 -1 5] es a) 1 x 4 b) 4 x 1 c) 4 x 4 d) 1 x 1
2) En la matriz A =
3) Si A =
4) Si A =
5) Si A =
6) Si A es una matriz de tamaño 5 x 2 y B es de tamaño 3 x 5, entonces el producto AT BT es de tamaño a)2 x 3 b)3 x 2 c)2 x 5 d) 5 x 5
7) Si A =
8) La matriz a) triangular superior b) triangular inferior c) simétrica d) diagonal
9) El tamaño de la matriz a) 2 x 3 b) 3 x 2 c) 6 x 1 d) 1 x 6
10) En la matriz A = a) 4 b) -4 c) 8 d) -5
11) La matriz a) triangular superior b) triangular inferior c) simétrica d) diagonal
12) La multiplicación escalar de la siguiente matriz, a la derecha es
II. Resuelve los siguientes ejercicios.
A) Realiza la suma de las siguientes matrices:
B. Realiza la resta de las siguientes matrices
C. Realiza la multiplicación de las siguientes matrices. D. Encuentra la multiplicación escalar:
E. Resuelve el siguiente ejercicio verbal: Pedro invirtió $10,000 parte al 6% de interés anual y el resto al 12% anual. ¿Cuánto debe invertir a cada por ciento de manera que obtenga el 8% de interés anual? Resuelve usando matrices.
APENDICE Contestación a la Pre y Pos Prueba I. Escoge la mejor contestación. 1) a 2) b 3) c 4) a 5) d 6) a 7) c 8) a 9) a 10) b 11) c 12) b 13) a
II. A: Suma de matrices 
B: Resta de matrices
C: Multiplicación de matrices.
D. Multiplicación Escalar
|
|















 es triangular inferior
es triangular inferior

 , hallar
, hallar












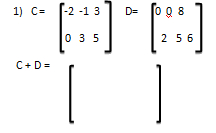











 entonces B- A es
entonces B- A es



 entonces 2A – 3B es igual a
entonces 2A – 3B es igual a


 es
es  el elemento a32 es
el elemento a32 es  es
es 







