MATEMÁTICAS INTEGRADAS 1

MODULO 4 LECCION 1

ELEMENTOS DE FUNCIONES

 Objetivos:

      Al finalizar el módulo el estudiante podrá:

o   Identificar si una ecuación, gráfica o conjunto de pares ordenados define una función.

o   Identificar la gráfica o ecuación que define una función.

o    Identificar cuando una función es creciente, decreciente o constante.

o   Evaluar una función de valor absoluto.

o   Graficar una función de valor absoluto.

o   Evaluar una ecuación de una función radical.

o   Graficar una función radical.

o   Identificar el dominio de una función.

o   Identificar el rango de una función,

o   Verificar si una gráfica de una función es par o impar.

o   Clasificar una función en par, impar o ninguna de las anteriores.

Observa las siguientes gráficas e indica. ¿Cuál crees que define una función?

¿Qué criterios usaste para identificarla?

Ahora sabrás que hay una prueba para identificar si una gráfica define una función. Esta prueba se conoce como prueba de la recta vertical.  Para llevar a cabo esta prueba sigue los siguientes pasos:

   Traza varias líneas verticales sobre cada una de las gráficas.

   Observa si cada línea trazada interseca sólo un punto de la gráfica.

   Si esto ocurre en todas las líneas trazadas sobre una sola  gráfica, entonces la gráfica define una función.

   Si al observar las líneas trazadas sobre una gráfica, al menos una de ellas interseca la gráfica por más

   de un punto, entonces la  gráfica no define una función?

   Puedes concluir que las gráficas B y D definen una función.

   DEFINICION

 Observa el siguiente conjunto de pares

ordenados:

El conjunto P:

En dicho conjunto se puede identificar el dominio y el rango.

El dominio(x) =

Rango(y) =

Este conjunto define una función dado

que no hay dos pares ordenados cuyo

primer componente (x) sea el mismo.

  El símbolo “ ” se lee: “f de x” o “el valor de f en x”.

Ejemplo:      

                         Evaluar: Sustituir (x) por el número 2         

 Práctica:

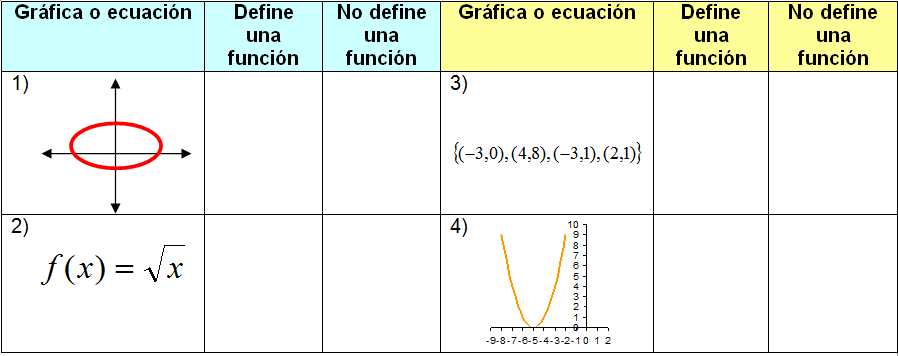
Observa detenidamente el contenido de la siguiente tabla.

En la primera columna hay una serie de gráfica, ecuaciones y conjuntos de pares

ordenados los cuales debes clasificar en: define una función o no define una función.

Haz una X en la columna que mejor la describa.

© Derechos Reservados

Escuela Virtual de Puerto Rico