
Por: Melissa Murrias
Revisado por: Dra. Luz M. Rivera
Una ecuación
cuadrática es una ecuación en su forma ax2 + bx
+ c, donde a, b, y c son números reales.
Ejemplo:
9x2 + 6x + 10 a = 9, b = 6, c = 10
3x2 - 9x a = 3, b = -9, c = 0
-6x 2 + 10
a = -6, b = 0, c = 10
Hay tres formas de hallar
las raíces ( el o los valores de la variable) de las ecuaciones
cuadráticas:
1. Factorización Simple
2. Completando el Cuadrado
3. Fórmula Cuadrática
Factorización Simple:
La factorización simple consiste en convertir la ecuación cuadrática en un producto de binomios. Luego, se busca el valor de x de cada binomio.
Ejemplo: Realizar la factorización simple de la ecuación
x2 + 2x – 8 =
0 a = 1
b = 2 c = - 8
(x
) (x ) = 0
[x ·x = x2]
| ( x + ) (x - ) = 0 |  |
(x + 4 ) (x – 2) = 0 4 y –2 4 + -2 = 2
![]() 4 · -2 = -8
4 · -2 = -8
x + 4 = 0
x – 2 = 0
x + 4 = 0
x – 2 = 0
x = 0 – 4
x = 0 + 2
x = -4
x = 2
Estas son las dos soluciones.
Completando el Cuadrado:
En este método,
la ecuación tiene que estar en su forma ax2+bx+c; y siempre
la constante de a tiene que ser igual a 1.
Por ejemplo, para
factorizar la ecuación 4x2 + 12x – 8 = 0, hay que despejar de la
siguiente forma:
|
4x2 + 12x – 8 = 0 4 4 4 4 |
x2 + 3x – 2 =
0 Ahora, a= 1.
Ejemplo:
x2 + 2x – 8 =
0 [Ya está
en su forma donde a = 1.]
x2 + 2x = 8
[ Pasar a c al lado opuesto.]
x2 + 2x + ___
= 8 + ___ [Colocar los blancos]
| x2 + 2x + 1 = 8 + 1 |  |
x2 + 2x + 1 = 9
(
) ( ) = 9
Hay que factorizar.
Nota: Siempre será un cuadrado perfecto.
| ( x + 1) (x + 1) = 9
(x + 1)2 = 9 (x + 1) = ±
|
 |
x + 1 = ± 3
x = -1 ± 3 [Separar las dos soluciones.]
x = -1 + 3
x = -1 – 3
x = 2
x = -4
Fórmula Cuadrática:
Este método
es muy simple: hay que sustituir los valores de a, b y c de la ecuación
cuadrática a la siguiente fórmula:
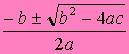
Ejemplo:
X2 + 2x – 8 =
0 a = 1, b = 2, c = -8


x = -2 ± 6
2
X = -2 + 6
x = -2 - 6
2
2
x = 4
x = -8
2
2
x = 2
x = - 4
Ir a ejercicios de Práctica