Problemas sin solución
Fecha de primera versión: 13-12-98
Fecha de última actualización: 19/04/2010
![]()
Todos los problemas que están en esta página se ha demostrado que no tiene solución, por lo tanto no perdáis ni un minuto intentando resolverlos.
Problema Délico (duplicación del cubo).
Dado un cubo cuya arista tiene longitud 1 se pide construir un cubo de volumen doble, utilizando regla (una regla sin marcas) y compás.
El nombre del problema se debe a que en Delfos (una isla griega) había un templo que era famoso por sus oráculos. Un rey acudió al templo para que le hiciesen un oráculo (adivinar el porvenir) y después de hacérselo le dijo a la sacerdotisa que le pidiese lo que quisiera. La sacerdotisa le pidió que construyese un altar del doble de volumen que el que tenía.
Se trata de calcular, con regla y compás un número que sea igual a la raíz cúbica de 2. La solución es un número irracional y con regla y compás sólo se pueden obtener números fraccionarios, por lo tanto es imposible.
Tendríamos que resolver la ecuación x3 = 2. No existe ningún número fraccionario que elevado al cubo dé 2.
Trisección de un ángulo.
Dado un ángulo alfa, se trata de dividirlo en tres partes iguales, utilizando regla y compás.
La trisección de un ángulo es equivalente a la resolución de la ecuación de tercer grado cos 3x = 4 (cos x)3 - 3 cos x.
Descartes resolvió este problema utilizando un compás como el de la figura
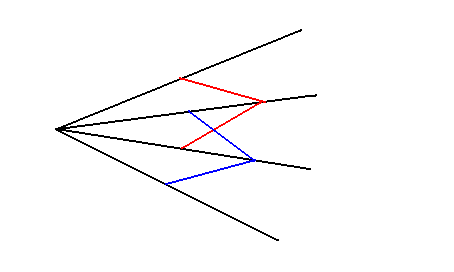
Las barras de colores rojo y azul están fijas en su extremo más cercano al vértice en un punto situado a la misma distancia en los cuatro brazos del compás. El otro extremo de las barras de colores se puede deslizar solidariamente con la barra compañera.
Rectificación de una circunferencia.
Dada una circunferencia de radio R, se trata de construir, con regla y compás, un segmento de longitud igual a la circunferencia.
Cuadratura del círculo.
Dado un círculo de radio R, se trata de construir, utilizando regla y compás, un cuadrado de igual superficie.
El primero que intentó resolver este problema fue Anaxágoras, mientras estaba en la cárcel como prisionero político (fue liberado gracias a la intervención de Pericles, de quien había sido profesor). Dicen que llenó las paredes de la celda con los cálculos.
Sea L el lado del cuadrado. Tendríamos L2 = p R2
El problema reside en la naturaleza de p.
Lindemann demostró que p no es solución de ningún polinomio y resulta que, con regla y compás, sólo se pueden construir cuadrados cuya longitud de lado sea un número algebráico, esto es, un número que sea solución de un polinomio.
Construcción de n-ágonos regulares.
Dado un círculo de radio R, se pide construir un n-ágono (un polígono de n lados) regular inscrito en él.
Este problema sólo tiene solución si n tiene la forma 2k +1.