Hipérbola

Fecha de primera versión: 02-04-98
Fecha de última actualización: 19/04/2010

La elipse, la parábola y la hipérbola se llaman secciones cónicas. La razón de este nombre es que estas curvas se forman al seccionar un cono por un plano.

Otra forma de definir estas curvas (en vez de como secciones de un cono) es como la curva que describe un punto que se mueve en un plano de manera que el cociente entre las distancias de ese punto a un punto fijo (foco) y a una recta (directriz) es constante (excentricidad).

Si esta constante está comprendida entre cero y uno, la curva es una elipse. Si es igual a uno, es una parábola y si es mayor que uno es una hipérbola.

Menaechmo, un discípulo de Platon y Eudoxo, estudió un caso especial de la hipérbola (xy = ab llamado hipérbola rectangular).

Euclides también estudió esta curva, pero ha pasado a la historia de la mano de Apolonio de Perga, al que debe su nombre.

Esta es la razón del nombre:

La parábola se puede expresar por esta ecuación y² = kx, siendo k = 2b²/a. Esto quiere decir que en cualquier punto de la parábola podemos construir un cuadrado de lado y (la ordenada del punto) y un rectángulo de lados x (la abscisa del punto) y k, y las áreas del cuadrado y el rectángulo siempre serán iguales.

Si hacemos lo mismo en una hipérbola el cuadrado siempre será mayor y en una parábola el cuadrado siempre es menor.

Resulta que una de las acepciones de parábola en griego era equiparable, de elipse deficiencia y de hipérbola exceso. De ahí los nombres.

Esto es una hipérbola (la figura en negro).

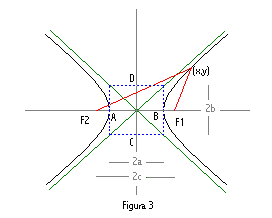
La propiedad de esta curva es que la diferencia de las distancias de cualquier punto de la hipérbola a dos puntos F1 y F2 (que se llaman focos) es constante.

El eje que pasa por los puntos A y B se llama eje real.

El eje que pasa por los puntos C y D se llama eje imaginario.

Los puntos A y B se llaman vértices.

Las rectas de color verde se llaman asíntotas (no sólo las hipérbolas tienen asíntotas).

La ecuación de la hipérbola es x²/a² - y²/b² = 1

La demostración de la ecuación de la hipérbola es muy sencilla: La distancia desde F2 (-c, 0) a un punto cualquiera (x, y) de la hipérbola es: y desde F1 (0, c) hasta el mismo punto (x, y) es: . Entonces, la diferencia de estas dos distancias es: . Elevando al cuadrado en los dos lados de la igualdad y haciendo una serie de cambios ingeniosos obtenemos la ecuación que hemos dado más arriba.

Las ecuaciones de las rectas directrices son:

x = a²/c
x = - a²/c

Las asíntotas de la hipérbola son:

y = b/a x
y = -b/a x 

La ecuación paramétrica de la hipérbola es:

x = a·chf
y = b·snf

Estas ecuaciones se deducen de la anterior teniendo en cuenta que ch²f - sh²f = 1. 

 

Cuando a = b la hipérbola se llama equilátera. En ese caso la ecuación es x² - y² = a² y las asíntotas son perpendiculares. Si utilizamos las asíntotas como ejes de coordenadas, la ecuación queda xy = a²/2.

 

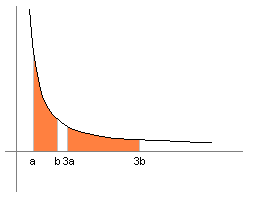
Este dibujo representa una rama de una hipérbola equilátera.

La ecuación de la hipérbola equilátera es la ecuación de la proporcionalidad inversa (dos variables son inversamente proporcionales cuando si dividimos una de ellas por una cantidad, la otra se multiplica por la misma cantidad. Supongamos la ecuación xy = 80, esto quiere decir que si x = 20, y = 4, si dividimos x por 10, y se tiene que multiplicar por 10, para que se siga manteniendo la igualdad).

La hipérbola equilátera tiene otra propiedad notable: si calculamos el área comprendida entre la hipérbola, el eje x y las verticales levantadas en dos puntos cualesquiera (a y b en el dibujo) y el área comprendida entre la hipérbola, el eje x y dos puntos situados n veces los anteriores (3a y 3b en el dibujo) veremos que son iguales.

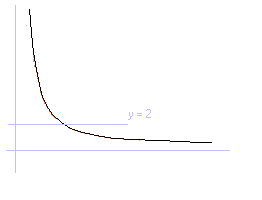
Otra propiedad importante: Si calculamos el área comprendida entre la hipérbola, la recta y = 2 y el eje Y, veremos que es infinito, sin embargo si calculamos el volumen generado por esa superficie al girar alrededor del eje Y, veremos que es finito.  

La ecuación de una hipérbola con centro en (x₀,y₀) y eje mayor paralelo al eje x es:

(x - x₀)²/a² - (y - y₀)²/b² = 1 

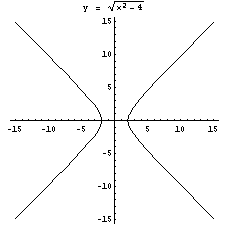
Propiedades de la hipérbola

La recta tangente en un punto es bisectriz del ángulo formado por los radios focales.

Construcción de la elipse

1- Dibuja una circunferencia en una hoja de papel.
2- Dibuja un punto fuera de la circunferencia (que no coincida con el centro).
3- Dobla la hoja de manera que cualquier punto de la circunferencia coincida con el punto dibujado.
4- Deshaz la doblez. 
5- Repite las operaciones 3 y 4 haciendo coincidir otro punto de la circunferencia. 

Las marcas que han dejado las dobleces delimitan una elipse. El punto dibujado es uno de los focos, el otro foco es el centro de la circunferencia.

Dibuja la curva.

En la página http://www-groups.dcs.st-and.ac.uk/~history/Curves/Curves.html encontrarás todo sobre las curvas.