Las matrices surgen del estudio de la resolución de los sistemas de ecuaciones
Sea el sistema de ecuaciones lineales:
a11x1 + ... + a1nxn = b1
a21x1 + ... + a2nxn = b2
....................................
am1x1 + ... + amnxn = bm
Los coeficientes de este sistema se pueden escribir de esta forma:
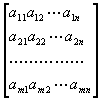
Un conjunto de N numeros dispuestos en n filas y m columnas, tal que n × m = N es un matriz.
Una matriz se suele representar por una letra mayuscula y los elementos de dicha matriz se representan por la correspondiente letra minuscula con dos subindices que indican la fila y columna.
Por ejemplo la matriz A y el elemento a12 (elemento de la fila 1, columna 2).Cuando el número de filas es igual al de columnas (n = m) la matriz se llama matriz cuadrada.
Cuando n = 1 la matriz se llama matriz fila.
Cuando m = 1 la matriz se llama matriz columna.
Las matrices fila y columna se llaman habitualmente vectores.
Cuando en una matriz cuadrada son ceros todos los elementos que no estan en la diagonal principal (la que va desde el angulo superior izquierdo al angulo inferior derecho) la matriz se llama matriz diagonal.
Si una matriz diagonal tiene todos los terminos de la diagonal iguales se llama matriz escalar.
Si una matriz diagonal tiene todos los terminos de la diagonal iguales a 1 se llama matriz unidad.
Las matrices cuadradas en las que aij = 0 siempre que i > j o bien aij = 0 siempre que i < j se llaman matrices triangulares.
Para sumar dos matrices tienen que tener las mismas dimensiones. Para sumar dos matrices se suman los elementos que ocupan las mismas posiciones
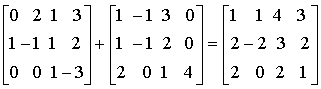
Para multiplicar un numero por una matriz, se multiplica cada elemento de la matriz por el número.
Para multiplicar dos matrices es indispensable que el número de columnas de la primera matriz sea igual al número de filas de la segunda matriz.
Dada una matriz, su traspuesta es la formada al disponer la fila 1 como columna 1, la fila 2 como columna 2... la fila n como columna n.
La traspuesta de la matriz A se designa por tA
El determinante de la matriz A se designa por |A|
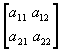
El determinante de esta matriz es a11× a22 - a12× a21
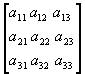
El determinante de esta matriz es a11× a22× a33 + a21× a32× a13 + a31× a12× a23 - a13× a22× a31 - a23× a32× a11 - a33× a21× a12
Los determinantes de una matriz y de su traspuesta son iguales. |A| = |tA|.
Si en una matriz se intercambian de posicion dos filas o dos columnas, el determinante cambia de signo.
Si se multiplican todos los elementos de una fila (o de una columna) por un número, el determinante queda multiplicado por ese número.
Si dos filas (o dos columnas) de una matriz son iguales, el determinante es cero.
Si dos filas (o dos columnas) de una matriz son proporcionales, el determinante es cero.
Si descomponemos en dos sumandos cada numero de una fila (o de una columna) de una matriz, la suma de los determinantes de las dos matrices obtenidas con la descomposicion en sumandos, es igual al determinante de la matriz original.
Si una fila (o columna) es combinacion lineal de las otras filas (o columnas) de una matriz, el determinante es cero.
Si cambiamos una fila (o una columna) por la obtenida por la suma de esa fila mas el producto de otra fila (o columna) por una constante, el determinante no varia.
Se pueden hacer transformaciones, siguiendo las reglas anteriores, en una matriz, de tal forma que, todos los elementos de una fila (o columna) sean ceros y el determinante no varie.
Menor complementario del elemento aij es el determinante de la matriz formada al suprimir la fila y la columna en la que esta el elemento aij.
El menor complementario de aij es aij.
Es el determinante de la matriz formada aplicando esta fórmula (-1)i+jaij.
La matriz inversa de A se designa por A-1
Para calcular la inversa de una matriz, primero se calcula su determinante. Si el determinante es cero la matriz no tiene inversa.
A continuacion se calculan los adjuntos de cada elemento de la matriz.
Despues se divide cada adjunto por el determinante de la matriz.
Despues se forma la matriz poniendo los valores obtenidos correspondientes a la posicion ij en la posicion ji
Vamos a calcular la inversa de la matriz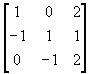
El determinante es 5 y la inversa

Dada una matriz, se puede obtener, suprimiendo algunas filas y columnas, otras matrices que se llaman submatrices. Si la submatriz es cuadrada y tiene k filas (tambien tendra k columnas), a su determinante se llama menor de orden k de la matriz dada.
Si el menor de orden k es distinto de cero, y todos los menores de orden k + 1 son cero, o no existen, a ese menor se llama menor principal de orden k.
El rango de una matriz A es el número natural k si k es el orden del mayor menor de la matriz A.
Un vector X (distinto de cero) es un vector propio de la matriz A si se cumple AX =lX. El número l se llama valor propio. Los vectores propios tambien se llaman autovectores y los valores propios autovalores.
Desarrollando la expresión AX =lX obtenemos el sistema:
(a11 - l)x1 + a12x2 + ... + a1nxn = 0
a21x1 + (a22- l)x2 + ... + a2nxn = 0
..........................................
an1x1 + an2x2 + ... + (ann- l)xn = 0