El volumen

Proyecto Salón Hogar

El volumen es otra propiedad física de la materia. Es el lugar que ocupa un cuerpo en el espacio. Se simboliza con la letra V y normalmente se asocia con el tamaño del cuerpo. Para medir el volumen se pueden utilizar distintos instrumentos, y las unidades en que se expresa pueden variar, dependiendo del estado en que se encuentre la materia. Veamos entonces.

Actividades

• Midamos el volumen de un líquido
• Midiendo el volumen de un sólido regular
• ¿Se puede medir el volumen de una piedra?
• ¿Podremos medir el volumen de un gas?

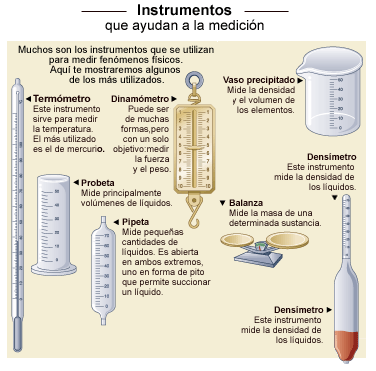
Unidades de volumen

Ver

ejercicios del

Sistema de medidas

Volumen en cuerpos poliédricos regulares

El volumen de un cuerpo regular es un número que se obtiene comparando el volumen del cuerpo con la unidad. Consideraremos a la unidad como un cubo de arista uno y por definición su volumen será 1. Entonces, la medida del volumen de un cuerpo será igual al número de cubos unitarios que contenga. Por ejemplo, considerando el cubo unidad que se indica en la figura, el cuerpo adjunto está formado por 25 cubos unidad. Podemos afirmar entonces que el cuerpo del ejemplo tiene 25 unidades de volumen .

Unidades de medida del volumen

Las unidades de volumen son estandarizaciones que permiten dimensionar el número que indica el volumen. Como unidad base, se considera a un cubo cuya arista mide un centímetro o un metro, un kilómetro, etc. Por definición su volumen tendrá el valor 1, acompañado de la unidad de su arista elevada a tres. Por ejemplo, en la figura siguiente, el volumen del cubo mide un centímetro cúbico y se abrevia por 1 cm³ .

Volumen del cubo unidad = 1 cm³

En la siguiente tabla se muestra las unidades de medida de volumen más utilizadas:  

Si la unidad de volumen del cubo unidad es el centímetro cúbico, entonces todos los volúmenes obtenidos a partir de él estarán en centímetros cúbicos. Se sigue la misma analogía si el cubo unidad tiene otra unidad de volumen.

Medición del volumen de algunos cuerpos simples con dos caras paralelas

• Volumen de un cubo

Un cubo es cuerpo formado por seis caras cuadradas y en cada vértice convergen 3 aristas mutuamente perpendiculares.

El volumen de un cubo es igual al valor de su arista elevada a tres, como muestra la siguiente figura: Si la arista del cubo adjunto mide 3 cm entonces su volumen se obtiene elevando a tres su arista:  

V_cubo=(3cm)³ = 3³ cm³ = 27cm³

Por lo tanto, si la arista de un cubo mide a, entonces su volumen se calcula a través de la fórmula:

El volumen a · a · a = a³ de un cubo se puede también definir como el producto del área de la cara basal a · a por la altura a, es decir:

V = a · a · a= (a · a ) · a =  a² · a  =  a³

• Volumen de un paralelepípedo

Un paralelepípedo es un cuerpo de seis caras pudiendo ser dos de ellas cuadradas (caras basales) y el resto rectangular (caras laterales). Si las caras laterales son perpendiculares a la altura del cuerpo entonces es le denomina paralelepípedo recto, en caso contrario se trata de un paralelepípedo oblicuo.

El volumen del paralelepípedo recto se calcula multiplicando las longitudes de las tres aristas convergentes a un vértice. Por ejemplo, si las aristas de un paralelepípedo recto son 2, 3 y 6 cm entonces el volumen del mismo se obtiene multiplicando 2 · 3 · 6:

Por lo tanto, si las tres aristas concurrentes a un vértice miden a, b y c entonces su volumen se calcula a través de la fórmula:

El volumen a · b · c de un paralelepípedo recto se puede también definir como el producto del área de la cara basal a · b por la altura c, es decir:

  V = (a · b ) · c =  a · b  · c

El procedimiento para calcular el volumen de un paralelepípedo oblicuo varía respecto al del paralelepípedo recto sólo en que la altura debe medirse en la perpendicular levantada desde el plano que contiene a base inferior hasta algún punto de la base superior, como muestra la línea roja en la figura adjunta.

Si las aristas de un paralelepípedo oblicuo son 2, 3 y 4 cm (como muestra la figura adjunta) entonces su  volu­men se obtiene multiplicando el área de la base (2 · 3 = 6) por la altura del mismo (6 · 4  = 24), es decir:

Por lo tanto, si las aristas de la base de un paralelepípedo miden a y b, y su altura mide h entonces su volumen se calcula a través de la fórmula del paralelepípedo recto:

El volumen a · b · h de un paralelepípedo oblicuo de aristas basales a, b y altura h también se puede definir como el producto del área de la cara basal a · b por la altura h, es decir,

V = (a · b ) · h =  a · b · h

• Volumen de un cilindro recto

Un cilindro recto, de base circular, es un cuerpo formado por dos caras circulares paralelas, como base, cuyos centros pertenecen a un segmento de recta perpendicular a ambos círculos, y por una superficie que las rodea por su borde, como muestra la figura adjunta.

El volumen de un cilindro recto de base circular de radio r y altura h se obtiene multiplicando el área de la circunferencia basal por la altura h.

Sabemos que el área de un círculo de radio r es:

A_círculo  =  p · r²

El volumen del cilindro cuya base es el círculo descrito anteriormente se obtiene multiplicando el área de dicho círculo por la altura del cilindro, es decir:

V_cilindro  =  A_círculo  · h              o sea:              

El volumen p · r² · h de un cilindro recto de base circular (con radio r) y altura h también se puede definir como el producto del área de la cara basal p · r² por la altura h, es decir,

V = (p · r²) · h = p · r² · h

• Volumen de un cilindro oblicuo de base circular

Un cilindro oblicuo, de base circular, es un cuerpo formado por dos caras circulares paralelas, como base, cuyos centros pasan por un segmento de recta que, a diferencia del cilindro recto, no es perpendicular a ambos círculos, y rodeado por una superficie que ajusta a los círculos, como muestra la figura adjunta.

El volumen de un cilindro oblicuo de base circular de radio r y altura h se obtiene multiplicando el área de la circunferencia basal por la altura h.

Sabemos que el área de un círculo de radio r es:

  A_círculo  =  p · r²

El volumen del cilindro cuya base es el círculo descrito anteriormente se obtiene multiplicando el área de dicho círculo por la altura del cilindro, es decir:

V_cilindro  =  A_círculo  · h              o sea:              

Podemos resumir el cálculo del volumen de paralelepípedos y cilindros en el siguiente esquema:

Medición del volumen de algunos cuerpos simples con sólo una cara de base

• Las pirámides

Una pirámide es un poliedro formado por un polígono, llamado base, y por caras laterales triangulares con un vértice común llamado vértice de la pirámide. Dependiendo del número de lados del polígono base (o equivalentemente del número de caras laterales) se clasifican en pirámides triangulares, cuadrangulares, etc.

•  Volumen de una pirámide recta de base cuadrada

Una pirámide recta de base cuadrada es aquella cuya base es un cuadrado de lado a y en la que el segmento bajado desde el vértice de la pirámide es perpendicular al plano de su base. Además, la longitud h de ese segmento se llama altura de la pirámide. Ver figura adjunta:

El volumen de la pirámide recta de base cuadrada se obtiene dividiendo por tres al producto entre su área basal a² y su altura h, es decir:  

• Volumen de una pirámide oblicua de base cuadrada

Una pirámide oblicua de base cuadrada es  aquella cuya base es un cuadrado de lado a y en la que el segmento bajado desde el vértice de la pirámide hasta su base no es perpendicular al plano de la base. La perpendicular bajada desde el vértice de la pirámide hasta su base (o al plano que contiene a la base) se llama altura de la pirámide. En la figura adjunta, la altura tiene longitud h.

El volumen de la pirámide oblicua de base cuadrada se obtiene de manera análoga al de las pirámides rectas, usando la misma fórmula, es decir:

• Volumen de conos rectos

La figura siguiente muestra un cono recto de radio basal r y altura h. La base del cono es un círculo, cuya área es:

A_círculo  =  p · r²

El volumen del cono recto corresponde a la tercera parte del producto entre el área de su base y su altura, es decir:

• Volumen de conos oblicuos

El cálculo del volumen en los conos oblicuos es análogo al de los cilindros rectos. Podemos observar en la figura adjunta, un cono oblicuo de altura h y radio basal r. Su volumen se obtiene, una vez más, de manera análoga al del cono recto y su fórmula es la misma:

Podemos resumir el cálculo del volumen de pirámides y conos en el siguiente esquema:

Medición del volumen de la esfera

El volumen de una esfera de radio r se obtiene a través de la  fórmula:

Arquímides ideó un método simple para determinar el volumen de la esfera. Imaginó una semiesfera, un cono y un cilindro juntos. Supuso que la esfera tenía radio R y tanto el cono como el cilindro con el mismo radio basal R. También supuso que las alturas del cono y el cilindro medían R como muestra la siguiente figura:

De estas figuras, son conocidos los volúmenes:

- Del cilindro: radio R y altura R, o sea  p·R²·R = p·R³  

- Del cono: radio R y altura R, o sea  (p·R²·R )/3 = (p·R³)/3

Luego cortó las tres figuras con un plano paralelo a la base del cilindro y del cono y a una distancia d de la parte superior de las figuras. Luego se preguntó cómo serían las secciones determinados por este plano en la semiesfera, el cono y el cilindro:

• La sección del cilindro

En el cilindro la sección que determina el plano es claramente un círculo de radio R y su área es:

• La sección de la semiesfera

 En la semiesfera, la sección circular que determina el plano que corta a la semiesfera, tiene un radio r (menor a R ) que depende de la distancia d. La siguiente figura muestra la situación:

El área del círculo de radio r, es:

Además, usando el Teorema de Pitágoras, en el triángulo rectángulo de lados R , d y r  se cumple que:

• La sección en el cono

El cono que consideró Arquímides, tiene altura y radio basal R, por lo tanto el triángulo formado por dicho radio basal, la altura y la pared del cono es rectángulo e isósceles. Por semejanza de triángulos, el circulo que determina el plano que corta al cono tiene radio d. La siguiente figura lo muestra:

En el cono, la sección que determina el plano, es un círculo de radio d y su área es:  

• Juntando las fórmulas

Hasta ahora sabemos que:

pero de la semiesfera obtuvimos que:

Si en el área del cilindro reemplazamos  R²  por  r² + d²  entonces tendremos que:

Es decir, la suma de las áreas de las secciones del cono y la semiesfera es igual al área de la sección del cilindro.

Esto ocurre para cualquier valor de d, por lo tanto, si consideramos las secciones (que forma el plano al cortar las figuras) como rebanadas finas, para cada trío de rebanadas tendríamos que:

Rebanada del cilindro = Rebanada de la semiesfera + Rebanada del cono

De la relación anterior podríamos suponer entonces que:  

Volumen del cilindro = Volumen de la semiesfera + Volumen del cono

y si reemplazamos en esta relación las fórmulas conocidas del volumen del cono y el cilindro, entonces es posible determinar el volumen de la semiesfera:

Despejando,

Por lo tanto, el volumen de la esfera es el doble del de la semiesfera:

El método de Arquímedes para encontrar el volumen de la esfera es simple e ingenioso. Arquímedes quedó tan maravillado con él, que dispuso grabar en su tumba esta figura, en recuerdo de su  idea:

 Clasificación de los cuerpos

 Se puede observar del diagrama que a partir de esta clasificación existen básicamente tres formas de calcular su volumen: el de los cilindros, el de las pirámides y el de la esfera.

Medición del volumen en cuerpos no regulares

• Por desplazamiento de líquido

Cuando un sólido no tiene una forma geométrica que permita determinar por cálculo su volumen, se mide éste directamente. El procedimiento se le atribuye a  Arquímedes.

Supongamos que se desea saber el volumen de una piedra pequeña. Por lo general las piedras tienen una forma muy irregular, por lo que es muy difícil calcular su volumen comparándolo con un cubo unidad. En estos casos se calcula su volumen por desplazamiento de agua.

En un recipiente graduado vertemos un líquido y, a continuación, sumergimos en él el sólido cuyo volumen deseamos conocer. El aumento de nivel del líquido nos permitirá, por sustracción, determinar el volumen del sólido. Normalmente el líquido empleado será agua, pero si el sólido se disuelve en ella (por ejemplo la sal o el azúcar) usaremos otro líquido que no disuelva al sólido.  

El siguiente diagrama muestra un objeto irregular y un recipiente con 9 centímetros cúbicos de agua. La cantidad de agua debe ser la suficiente para que el objeto pueda ser sumergido en ella.

Se introduce el objeto en el recipiente y se mide el desplazamiento de agua que provocó:

Al introducir el objeto al recipiente el agua subió su nivel marcando un volumen de 11 cm ³. Antes de introducirlo el volumen del agua marcaba 9 cm ³ por lo que la diferencia de volumen se debe al objeto.

El volumen del objeto se obtiene restando el volumen del agua, con el objeto, menos el volumen del agua sin el objeto:

 V   =  11 cm ³    -     9 cm ³    =    2 cm ³

Por lo tanto el objeto tiene un volumen de 2 cm ^3.  

Este método es bastante sencillo, pero es útil sólo para objetos pequeños que no absorben el líquido en el que son sumergidos. No es posible usarlo para medir el volumen de una pirámide Egipcia, por ejemplo.

• Principio de Cavalieri

Otra manera de conocer el volumen de un sólido cuando no tiene una forma geométrica que permita calcular su volumen a través de las fórmulas vistas es usa. Veamos un ejemplo que visualiza este principio.

Usando tres montoncitos de 15 fichas (monedas de $10 u objetos similares, todos iguales) y una cinta de cartulina cuyo ancho sea mayor que el diámetro de las fichas, ordena las fichas en 3 pilas de modo que sólo una sea recta y las otras dos sean oblicuas o sinuosas y a continuación pasa la cinta entre las fichas a la misma altura en las tres pilas.

Notarás que las áreas de las fichas que tocan la cinta son iguales para las tres pilas y si pasas la cinta a cualquier otra altura, las áreas de las fichas siguen siendo iguales. El Principio de Cavalieri asegura que si esto ocurre para cualquier altura entonces las tres pilas tienen el mismo volumen.