|
Á
L G E B R A

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
Sumar ecuaciones con
enteros de 3 dígitos
Una
ecuación es una aseveración matemática tal que la _expresión
en el lado izquierdo del signo igual (=) tiene el
mismo valor que la _ expresión en el lado derecho.
Un ejemplo de una ecuación es 200 + (-600) = - 400.
Uno
de los términos de una ecuación puede ser
desconocido y necesite ser determinado. A menudo
este término desconocido es representado por una
letra tal como x (e.g. 200 + x =- 400)
La
solución de una ecuación es encontrar el valor de la
incógnita x. Para encontrar el valor de x podemos
usar la propiedad de la resta de la ecuación que
dice: Los dos miembros de una ecuación permanecen
iguales si se resta el mismo número a cada miembro.
También podemos usar la propiedad aditiva de la
ecuación que dice: Los dos miembros de la una
ecuación permanecen igual si se suma el mismo número
a cada miembro.
Ejemplo:
- 500 + x = 400
- 500 + x + 500 = 400 + 500
0 + x = 900
x = 900
Verifica el resultado sustituyendo la respuesta
(900) nuevamente en la ecuación.
- 500 + 900 = 400
Sumar ecuaciones con enteros de 4
dígitos
Una
ecuación es una aseveración matemática tal que la _expresión
en el lado izquierdo del signo igual (=) tiene el
mismo valor que la _ expresión en el lado derecho.
Un ejemplo de una ecuación es 2000 + (-6000) = -
4000
Uno
de los términos de una ecuación puede ser
desconocido y necesite ser determinado. A menudo
este término desconocido es representado por una
letra tal como x (e.g. 2000 + x =- 4000).
La
solución de una ecuación es encontrar el valor de la
incógnita x. Para encontrar el valor de x podemos
usar la propiedad de la resta de la ecuación que
dice: Los dos miembros de una ecuación permanecen
iguales si se resta el mismo número a cada miembro.
También podemos usar la propiedad aditiva de la
ecuación que dice: Los dos miembros de la una
ecuación permanecen igual si se suma el mismo número
a cada miembro.
Ejemplo:
- 5000 + x = 4000
- 5000 + x + 5000 = 4000 + 5000
0 + x = 9000
x = 9000
Verifica el resultado sustituyendo la respuesta
(9000) nuevamente en la ecuación.
- 5000 + 9000 = 4000
Ecuaciones de restas enteras
Restar ecuaciones – Enteros de 1
dígito
Una
ecuación es un enunciado matemático tal que la
expresión a la izquierda del signo igual (=) tenga
el mismo valor que la expresión a la derecha. Un
ejemplo de una ecuación es - 2 -(-6) = 4.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser averiguado. Con
frecuencia el término desconocido se representa con
una letra tal como x. (ej. - 2 + x = 4).
La
solución de una ecuación es encontrar el valor de la
incógnita x. Para encontrar el valor de x podemos
utilizar la propiedad de la resta de la ecuación que
dice: Los dos lados de una ecuación se mantienen
igual si se resta el mismo número a ambos lados.
También podemos utilizar la propiedad de la suma de
la ecuación que dice: Los dos lados de una ecuación
se mantienen igual si se suma el mismo número a
ambos lados.
Ejemplo:
x - (- 5) = 4
x + 5 = 4
x + 5 - 5 = 4 - 5
x + 0 = - 1
x = - 1
Verifica el resultado sustituyendo la x por el
resultado ( -1) en la ecuación original.
- 1 - ( - 5) = 4
Restar ecuaciones – Enteros de 2
dígitos
Una
ecuación es un enunciado matemático tal que la
expresión a la izquierda del signo igual (=) tenga
el mismo valor que la expresión a la derecha. Un
ejemplo de una ecuación es - 20 -(-60) = 40.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser averiguado. Con
frecuencia el término desconocido se representa con
una letra tal como x. (ej. - 20 + x = 40).
La
solución de una ecuación es encontrar el valor de la
incógnita x. Para encontrar el valor de x podemos
utilizar la propiedad de la resta de la ecuación que
dice: Los dos lados de una ecuación se mantienen
igual si se resta el mismo número a ambos lados.
También podemos utilizar la propiedad de la suma de
la ecuación que dice: Los dos lados de una ecuación
se mantienen igual si se suma el mismo número a
ambos lados.
Ejemplo:
x - (- 50) = 40
x + 50 = 40
x + 50 - 50 = 40 - 50
x + 0 = - 10
x = - 10
Verifica el resultado sustituyendo la x por el
resultado ( -10) en la ecuación original.
- 10 - ( - 50) = 40
Restar ecuaciones – Enteros de 3
dígitos
Una
ecuación es un enunciado matemático tal que la
expresión a la izquierda del signo igual (=) tenga
el mismo valor que la expresión a la derecha. Un
ejemplo de una ecuación es - 200 -(-600) = 400.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser averiguado. Con
frecuencia el término desconocido se representa con
una letra tal como x. (ej. - 200 + x = 400).
La
solución de una ecuación es encontrar el valor de la
incógnita x. Para encontrar el valor de x podemos
utilizar la propiedad de la resta de la ecuación que
dice: Los dos lados de una ecuación se mantienen
igual si se resta el mismo número a ambos lados.
También podemos utilizar la propiedad de la suma de
la ecuación que dice: Los dos lados de una ecuación
se mantienen igual si se suma el mismo número a
ambos lados.
Ejemplo:
x - (- 500) = 400
x + 500 = 400
x + 500 - 500 = 400 - 500
x + 0 = - 100
x = - 100
Verifica el resultado sustituyendo la x por el
resultado ( -100) en la ecuación original.
- 100 - ( - 500) = 400
Resta de ecuaciones – Enteros de
4 dígitos
Una
ecuación es un enunciado matemático tal que la
expresión a la izquierda del signo igual (=) tenga
el mismo valor que la expresión a la derecha. Un
ejemplo de una ecuación es - 2000 -(-6000) = 4000.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser averiguado. Con
frecuencia el término desconocido se representa con
una letra tal como x. (ej. - 2000 + x = 4000).
La
solución de una ecuación es encontrar el valor de la
incógnita x. Para encontrar el valor de x podemos
utilizar la propiedad de la resta de la ecuación que
dice: Los dos lados de una ecuación se mantienen
igual si se resta el mismo número a ambos lados.
También podemos utilizar la propiedad de la suma de
la ecuación que dice: Los dos lados de una ecuación
se mantienen igual si se suma el mismo número a
ambos lados.
Ejemplo:
x - (- 5000) = 4000
x + 5000 = 4000
x + 5000 - 5000 = 4000 - 5000
x + 0 = - 1000
x = - 1000
Verifica el resultado sustituyendo la x por el
resultado ( -1000) en la ecuación original.
- 1000 - ( - 5000) = 4000
Ecuaciones con
multiplicación
Una
ecuación es un enunciado matemático tal que la _expresión
a la izquierda del signo igual (0) tenga el mismo
valor que la _expresión a la derecha. Un ejemplo de
una ecuación es 9 * 8 = 72.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser determinado. El término
desconocido se puede representar con un letra tal
como x. (es decir x * 8 = 72).
La
solución de una ecuación es averiguar el valor de la
incognita x. Usa la propiedad de división de
ecuaciones para averiguar el valor de x. La
propiedad de división de ecuaciones dice que los dos
lados de la ecuación se mantienen igual si ambos
lados se dividen por el mismo número.
Ejemplo:
x * 5 = 10
x * 5 ÷ 5 = 10 ÷ 5
x * 1 = 2
x = 2
Verifica el resultado sustituyendo la respuesta (2)
nuevamente en la ecuación.
2 * 5 = 10
Una
ecuación es un enunciado matemático tal que la _expresión
a la izquierda del signo igual (0) tenga el mismo
valor que la _expresión a la derecha del signo. Un
ejemplo de una ecuación es 12 * 11 = 132.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser determinado. El término
desconocido se puede representar por una letra tal
como x. (es decir x * 11 = 132)
La
solución de una ecuación es averiguar el valor de la
incognita x. Usa la propiedad de división de
ecuaciones para averiguar el valor de x. La
propiedad de división de ecuaciones dice que los dos
lados de la ecuación se mantienen igual si ambos
lados se dividen por el mismo número.
Ejemplo:
x * 50 = 1000
x * 50 ÷ 50 = 1000 ÷ 50
x * 1 = 20
x = 20
Verifica el resultado sustituyendo la respuesta (20)
nuevamente en la ecuación.
20 * 50 = 1000
Ecuaciones
con division
Una
ecuación es un enunciado matemático tal que la
expresión del lado izquierdo del signo igual tenga
el mismo valor que la expresión en el lado derecho.
Un ejemplo de una ecuación es 72 ÷ 8 = 9.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser averiguado. El término
desconocido se puede representar por una letra tal
como x, (e.g. x ÷ 8 = 9).
La
solución de una ecuación es encontrar el valor de la
incognita x. Utiliza la propiedad de la
multiplicación de ecuaciones para encontrar el valor
de x. La propiedad de la multiplicación de
ecuaciones dice que los dos lados de una ecuación se
mantienen iguales si ambos lados se multiplican por
el mismo número.
Ejemplo:
x ÷ 5 = 2
x ÷ 5 * 5 = 2 * 5
x ÷ 1 = 10
x = 10
Verifica el resultado sustituyendo la x por el
resultado (10).
10 ÷ 5 = 2
División de ecuaciones con
números de 2 dígitos
Una
ecuación es un enunciado matemático tal que la
expresión en el lado izquierdo del signo igual (=)
tenga el mismo valor que la expresión en el lado
derecho. Un ejemplo de una ecuación es 132 ÷ 12 =
11.
Uno
de los términos en una ecuación puede ser
desconocido y necesite ser averiguado. El término
desconocido se puede representar por una letra tal
como x. (ej. x ÷ 12 = 11).
La
solución de una ecuación es encontrar el valor de la
incognita x. Usa la propiedad de la multiplicación
de la ecuación para encontrar el valor de x. La
propiedad de la multiplicación de la ecuación dice
que los dos lados de una ecuación se mantienen
iguales si ambos lados se multiplican por el mismo
número.
Ejemplo:
x ÷ 50 = 20
x ÷ 50 * 50 = 20 * 50
x ÷ 1 = 1000
x = 1000
Verifica el resultado sustituyendo la x por el
resultado (1000).
1000 ÷ 50 = 20
Números Reales
Los números que se utilizan en el álgebra son los
números reales. Hay un número real en cada punto de la recta numérica. Los
números reales se dividen en números racionales, números irracionales y numeros
enteros los cuales a su vez se dividen en números negativos, números positivos y
cero (0) .Podemos verlo en esta tabla:

Un número real es racionalsi
se puede representar como cociente a/b, donde
a sea un entero y b sea un entero no igual a cero. Los números
racionales pueden escribirse en forma decimal.
Existen dos maneras:
X decimales terminales
X decimales que se repiten infinitamente
Los números reales que no pueden ser expresados en
la forma
a/b, donde a y b son enteros se llaman números
irracionales.
Los números irracionales no tienen decimales terminales ni decimales que
se repiten infinitamente.
Orden de Operaciones
- Primero resolver todo lo que esté dentro de
simbolos de agrupación.
- Evaluar las expresiones exponenciales.
- Hacer todas las multiplicaciones y divisiones
en orden de izquierda a derecha.
- Hacer todas las sumas y restas en orden de
izquierda a derecha.
Ejemplo:

Reglas de los Signos:
- En suma de números con signos iguales, se
suman los números y el resultado lleva el mismo signo. Si los números tienen
signos diferentes, se restan y el resultado lleva el signo del mayor.
- Ejemplo:
- 5 + 8 = 13
- 5 + -8 = -3
- En resta de signos iguales el resultado lleva
el signo del mayor. Si se restan signos diferentes, se suman los números y el
resultado lleva el signo del mayor.
- Ejemplo:
- 5 - 8 = -3
- 5 - (-8) = 13
- En multiplicación y división de números con
signos iguales el resultado es positivo. Si los números son signos opuestos, el
resultado es negativo.
- Ejemplo:
- 5 x 8 = 40
- 5 x -8 = -40
Recta Numérica
Para construir una recta
numérica, primero se escoge un punto en la recta que será un punto
arbitrario al que le llamaremos cero (0). Este punto es llamado el origen de la
recta numérica. El origen separa la recta en dos partes, el lado positivo y el
lado negativo. A la derecha del origen está el lado positivo y el negativo está
a la izquierda. En el lado derecho van números enteros positivos (en orden
sucesivo) y en el lado izquierdo se escriben los números enteros negativos (en
orden sucesivo), estos se marcan en unidades equidistantes.
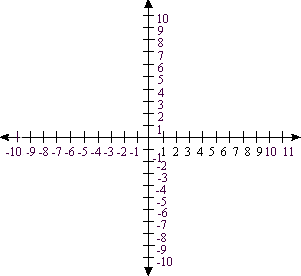
Es importante recordar que para cualesquiera dos
números reales diferentes a los que llamaremos a y b, siempre uno
es mayor que el otro.
- Si a - b es positivo, entonces a > b.
- Si b - a es positivo, entonces a < b.
Valor Absoluto
La distancia de un número en la recta numérica
desde cero (0) se llama valor absoluto. Se
representa con el simbolo |x|. El valor absoluto de un número se calcula de la
siguiente manera:
- si el número es negativo, lo convertimos a
positivo.
- si el número es cero o positivo, se queda
igual.
Ejemplos:
|7| = 7
|-7| = 7
Notación Exponencial
La notación exponencial
se usa para repetir multiplicaciones de un mismo número. Es la elevación
a la enésima potencia (n) de una base (X).

Ejemplos:
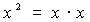
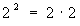
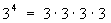
Expresiones Algebraicas
Las expresiones algebraicas se clasifican según su
número de términos.
monomio = un solo
término.

Por ejemplo:
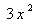
binomio
= suma o resta de dos monomios.
Por ejemplo:
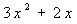
trinomio = suma o
resta de tres monomios.
Por ejemplo:
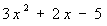
polinomio = suma o
resta de cualquier número de monomios.
- Para multiplicar factores exponenciales que
tienen la misma base y los exponentes son enteros positivos diferentes.

- Ejemplo:
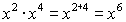
- Para multiplicar factores que tienen base
diferente y exponentes iguales, el exponente se queda igual.

- Ejemplo:
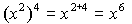
- En división, si tienen la misma base y los
exponentes son enteros positivos diferentes, se restan los exponentes. Las
variables m y n son enteros positivos , m > n.

- Ejemplo:
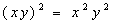
- En suma y resta, solo se procede si son
términos similares, en otras palabras lo que difiere es su coeficiente numérico.
Productos
Especiales
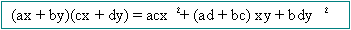
Por ejemplo:
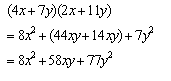
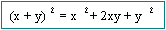
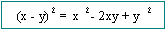
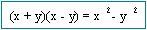
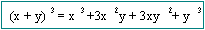
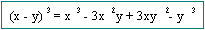
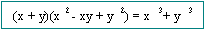

Factorización de Polinomios
Factorizar un polinomio
es el primer método para obtener las raíces o ceros de la expresión. Para
factorizar se comienza con una regla que te permite desarrollar la destreza,
para aplicarla a ejercicios de mayor dificultad. Se buscan dos factores o
números cuyo producto sea el último término y a la vez sumados o restados den
como resultado el coeficiente del término del medio. Esta regla aplica solo a
ecuaciones cuadráticas cuyo coeficiente de la variable elevado al cuadrado es 1.
Si el coeficiente de la variable elevada al cuadrado no fuese 1, la manera de
factorizar sería tanteando hasta poder lograr la factorización. Muchas veces la
factorización es simplemente reconocer factores comunes.
Se puede utilizar también la inversa de las fórmulas de productos especiales. O
sea, expresamos el polinomio como una multiplicación o un producto, usando las
fórmulas a la inversa.
Completando el Cuadrado
Completando el cuadrado
es el segundo método para obtener las raíces o ceros de un polinomio. El proceso
es el siguiente:
- Primero mueves el tercer término con signo
opuesto al lado contrario de la igualdad.
- Luego, vas a calcular el término que te
permite crear tu cuadrado de la siguiente forma: selecciona el coeficiente de la
variable que está elevada a la 1, se divide entre dos y elevarlo al cuadrado.
- Este resultado lo sumarás a ambos lados de la
expresión.
- Después, la raíz cuadrada del primer término,
el operador (signo) del medio y la raíz cuadrada del último termino, todo
elevado al cuadrado es igual a la suma de la derecha.
- Luego, sacas raíz cuadrada a ambos lados,
observando que hay dos posibles soluciones, el caso positivo y el caso negativo.
- Por último despejas por la variable y esas son
las raíces o ceros del polinomio.
Como ejemplo vamos a utilizar el ejercicio  . .


Expresiones Fraccionales
Una fracción
es una expresión en la forma:

Una expresión fraccional esta simplificada cuando
el numerador y el denominador no tienen factores comunes.
Por ejemplo:
 Para multiplicar expresiones fraccionales, se
multiplican los numeradores y se multiplican los denominadores.
Para multiplicar expresiones fraccionales, se
multiplican los numeradores y se multiplican los denominadores.

Por ejemplo:
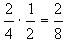
Para dividir se multiplica por el reciproco y luego se factoriza y se simplifica
el resultado.

Por ejemplo:
 En suma y resta cuando los denominadores son los
mismos, se suman o restan los numeradores y se mantiene el mismo denominador.
En suma y resta cuando los denominadores son los
mismos, se suman o restan los numeradores y se mantiene el mismo denominador.

Por ejemplo:
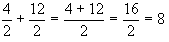
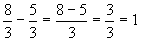
Exponentes Enteros
Radicales
Un radical es
una expresión en la forma:
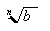
Cada parte de un radical lleva su nombre,
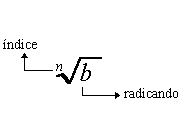
El índice debe ser un entero positivo. Para una raíz cuadrada, el índice 2 es
usualmente omitido.
Propiedades de los Radicales
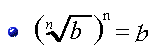
Ejemplo:
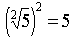
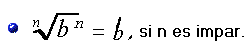
Ejemplo:
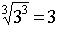
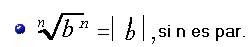
Ejemplo:
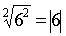
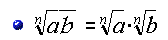
Ejemplo:
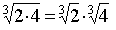
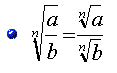
Ejemplo:


Suma y Resta de Radicales
Cuando tenemos radicales "semejantes", podemos
resolver la suma o la resta usando la propiedad distributiva y agrupando los
términos semejantes. Los radicales "semejantes"
son los que tienen el mismo radicando.
Ejemplos:
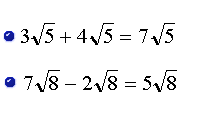
Si los radicales no son semejantes, la suma o la
resta solo puede ser indicada. Se puede agrupar los términos semejantes del
radical.
Ejemplo:
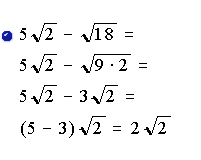

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|